题目内容
如图，△ABC中，E、D分别是AC、BC的中点，AD、BE交于点O，则S△DOE：S△AOB=（ ）| A、1：2 | B、2：3 |
| C、1：3 | D、1：4 |
考点：相似三角形的判定与性质
专题：
分析：根据三角形中位线定理可得DE=
AB，DE∥AB，再根据平行线性质和相似三角形的判定与性质即可求解．
| 1 |
| 2 |
解答：解：∵△ABC中，E、D分别是AC、BC的中点，
∴DE=
AB，DE∥AB，
∴△DOE∽△AOB，
∴S△DOE：S△AOB=1：4．
故选：D．
∴DE=
| 1 |
| 2 |
∴△DOE∽△AOB，
∴S△DOE：S△AOB=1：4．
故选：D．
点评：该题主要考查了三角形中位线定理、平行线的性质、相似三角形的判定与性质等几何知识点及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
【问题情境】一次知识竞赛共有20道选择题，规定答对一道得5分，不做或错一题扣1分，结果某学生得分为88分，则他做对题数为（ ）
| A、16 | B、17 | C、18 | D、19 |
如图，已知直线AB、DE相交于点O，∠AOC=160°，OC平分∠EOB，试求∠AOD的度数．下列说法中正确的是（ ）
| A、若|a|=|b|，则a=b |
| B、若ac=bc，则a=b |
| C、若线段AC=BC，则点C是线段AB的中点 |
| D、过n边形的一个顶点有（n-3）条对角线 |
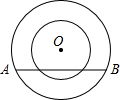如图，以O为圆心的两个同心圆中，半径分别为3和5，若大圆的弦AB与小圆相交，则弦AB的长的取值范围是（ ）| A、8≤AB≤10 |
| B、8＜AB＜10 |
| C、8＜AB≤10 |
| D、6≤AB≤10 |
下面四个数中，最小的数是（ ）
| A、-2 | ||
| B、0 | ||
| C、0.2 | ||
D、-
|