题目内容
某项工程,若由乙队独做2天后,再由甲、乙两队合做10天能完成全部工程.已知乙队每天的工效比甲队高25%.甲队每天的工程费3万,乙队每天的工程费3.5万.
①求甲、乙两队单独完成此项工程各需多少天?
②如果工程要求不超过12天完工,那么,在尽可能节约施工费用的情况下,该怎样安排甲乙两对施工?最低工程费是多少万元.
①求甲、乙两队单独完成此项工程各需多少天?
②如果工程要求不超过12天完工,那么,在尽可能节约施工费用的情况下,该怎样安排甲乙两对施工?最低工程费是多少万元.
考点:分式方程的应用
专题:
分析:①设甲单独做需要x天完成,则甲的工作效率是
,乙的工作效率是
,等量关系是2×乙的工作效率+10(甲的工作效率+乙的工作效率)=1;
②首先求得甲队与乙队单独施工的天数,再进一步算出各自的施工总费用,找出12天全部施工的单位,再进一步列出方程解决问题.
| 1 |
| x |
| 5 |
| 4x |
②首先求得甲队与乙队单独施工的天数,再进一步算出各自的施工总费用,找出12天全部施工的单位,再进一步列出方程解决问题.
解答:解:①设甲单独做需要x天完成,则
2×
+10×(
+
)=1,
解得 x=25.
则 25×
=20(天).
答:甲、乙两队单独完成此项工程分别需要25天、20天;
②甲队单独完成工程费用为3×25=75(万元),乙队单独完成工程费用为3.5×20=70(万元),
因此可以看到,安排乙队单独施工费用更低.
但乙队单独施工无法在12天完工,因此将工期按12天处理,尽可能安排乙队施工会节省费用
所以设甲队施工y天,则
+
=1,
解得y=10.
因此安排甲乙合作施工10天,乙队单独施工2天可以尽可能节省费用.
10×3+12×3.5=76(万元).
答:安排甲乙合作施工10天,乙队单独施工2天可以尽可能节省费用,最低费用是76万元.
2×
| 5 |
| 4x |
| 1 |
| x |
| 5 |
| 4x |
解得 x=25.
则 25×
| 4 |
| 5 |
答:甲、乙两队单独完成此项工程分别需要25天、20天;
②甲队单独完成工程费用为3×25=75(万元),乙队单独完成工程费用为3.5×20=70(万元),
因此可以看到,安排乙队单独施工费用更低.
但乙队单独施工无法在12天完工,因此将工期按12天处理,尽可能安排乙队施工会节省费用
所以设甲队施工y天,则
| y |
| 25 |
| 12 |
| 20 |
解得y=10.
因此安排甲乙合作施工10天,乙队单独施工2天可以尽可能节省费用.
10×3+12×3.5=76(万元).
答:安排甲乙合作施工10天,乙队单独施工2天可以尽可能节省费用,最低费用是76万元.
点评:此题考查分式方程与一元一次方程的实际运用,掌握题目中蕴含的数量关系是解决问题的关键.

练习册系列答案
相关题目
用配方法解方程x2-2x-5=0方程可变形为( )
| A、(x+1)2=4 |
| B、(x-1)2=4 |
| C、(x+1)2=6 |
| D、(x-1)2=6 |
 如图,△EFG≌△NMH,在△EFG中,FG是最长的边,在△NMH中,MH是最长的边,∠F和∠M是对应角,且EF=2.4cm,FH=1.9cm,HM=3.5cm.
如图,△EFG≌△NMH,在△EFG中,FG是最长的边,在△NMH中,MH是最长的边,∠F和∠M是对应角,且EF=2.4cm,FH=1.9cm,HM=3.5cm.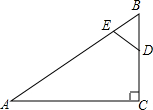 如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<15),连接DE,当△BDE是直角三角形时,t的值为
如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<15),连接DE,当△BDE是直角三角形时,t的值为