题目内容
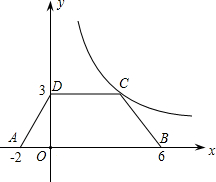 如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.(1)直接写出点C的坐标;
(2)求反比例函数的解析式;
(3)将等腰梯形ABCD向上平移m个单位后,使点B恰好落在曲线上,求m的值.
考点:反比例函数综合题
专题:
分析:(1)过点C作CE⊥AB于点E,根据HL证Rt△AOD≌Rt△BEC,求出OA=BE=2,即可求出C的坐标;
(2)设反比例函数的解析式为:y=
,将点C的坐标代入反比例函数的解析式求出k即可;
(3)当点B恰好落在曲线上时,得出此时B的坐标是(6,m),代入反比例函数的解析式,即可求出答案.
(2)设反比例函数的解析式为:y=
| k |
| x |
(3)当点B恰好落在曲线上时,得出此时B的坐标是(6,m),代入反比例函数的解析式,即可求出答案.
解答:解:(1)过点C作CE⊥AB于点E,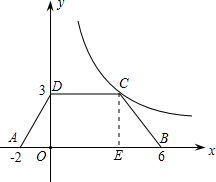
∵四边形ABCD是等腰梯形,
∴AD=BC,DO=CE,
∵∠DOA=∠CEO=90°,
在Rt△AOD和Rt△BEC中,
,
∴Rt△AOD≌Rt△BEC(HL),
∴AO=BE=2,
∵BO=6,
∴DC=OE=4,
∴C(4,3);
(2)设反比例函数的解析式为:y=
,
根据题意得:3=
,
解得:k=12,
∴反比例函数的解析式为:y=
,
即反比例函数的解析式是y=
;
(3)将等腰梯形ABCD向上平移m个单位后点B恰好落在曲线上,
∴点B(6,m),
∵点B(6,m)恰好落在双曲线y=
上,
∴当x=6时,m=
=2,即m=2.

∵四边形ABCD是等腰梯形,
∴AD=BC,DO=CE,
∵∠DOA=∠CEO=90°,
在Rt△AOD和Rt△BEC中,
|
∴Rt△AOD≌Rt△BEC(HL),
∴AO=BE=2,
∵BO=6,
∴DC=OE=4,
∴C(4,3);
(2)设反比例函数的解析式为:y=
| k |
| x |
根据题意得:3=
| k |
| 4 |
解得:k=12,
∴反比例函数的解析式为:y=
| 12 |
| x |
即反比例函数的解析式是y=
| 12 |
| x |
(3)将等腰梯形ABCD向上平移m个单位后点B恰好落在曲线上,
∴点B(6,m),
∵点B(6,m)恰好落在双曲线y=
| 12 |
| x |
∴当x=6时,m=
| 12 |
| 6 |
点评:本题考查了用待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,全等三角形的性质和判定,等腰梯形的性质的应用,通过做此题培养学生运用性质进行计算的能力,题型较好,难度也适中.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
下列说法中正确的是( )
| A、若|a|=|b|,则a=b |
| B、若ac=bc,则a=b |
| C、若线段AC=BC,则点C是线段AB的中点 |
| D、过n边形的一个顶点有(n-3)条对角线 |
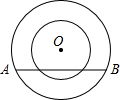 如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )
如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )| A、8≤AB≤10 |
| B、8<AB<10 |
| C、8<AB≤10 |
| D、6≤AB≤10 |
下面四个数中,最小的数是( )
| A、-2 | ||
| B、0 | ||
| C、0.2 | ||
D、-
|
 如图是一个几何体的俯视图,则该几何体可能是( )
如图是一个几何体的俯视图,则该几何体可能是( )A、 |
B、 |
C、 |
D、 |
 如图,∠B与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C进行同样的讨论.
如图,∠B与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C进行同样的讨论.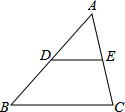 如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为
如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为 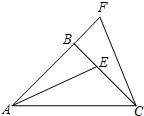 如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF