题目内容
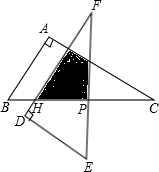 如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为
如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为考点:旋转的性质
专题:计算题
分析:如图,由点P为斜边BC的中点得到PC=
BC=6,再根据旋转的性质得PF=PC=6,∠FPC=90°,∠F=∠C=30°,根据含30度的直角三角形三边的关系,在Rt△PFH中计算出PH=
PF=2
;在Rt△CPM中计算出PM=
PC=2
,且∠PMC=60°,则∠FMN=∠PMC=60°,于是有∠FNM=90°,FM=PF-PM=6-2
,则在Rt△FMN中可计算出MN=
FM=3-
,FN=
MN=3
-3,然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH-S△FMN进行计算即可.
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答: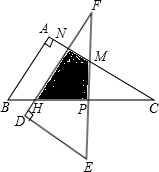 解:如图,
解:如图,
∵点P为斜边BC的中点,
∴PB=PC=
BC=6,
∵△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,
∴PF=PC=6,∠FPC=90°,∠F=∠C=30°,
在Rt△PFH中,∵∠F=30°,
∴PH=
PF=
×6=2
,
在Rt△CPM中,∵∠C=30°,
∴PM=
PC=
×6=2
,∠PMC=60°,
∴∠FMN=∠PMC=60°,
∴∠FNM=90°,
而FM=PF-PM=6-2
,
在Rt△FMN中,∵∠F=30°,
∴MN=
FM=3-
,
∴FN=
MN=3
-3,
∴△ABC与△DEF重叠部分的面积=S△FPH-S△FMN
=
×6×2
-
(3-
)(3
-3)
=9(cm2).
故答案为9.
 解:如图,
解:如图,∵点P为斜边BC的中点,
∴PB=PC=
| 1 |
| 2 |
∵△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,
∴PF=PC=6,∠FPC=90°,∠F=∠C=30°,
在Rt△PFH中,∵∠F=30°,
∴PH=
| ||
| 3 |
| ||
| 3 |
| 3 |
在Rt△CPM中,∵∠C=30°,
∴PM=
| ||
| 3 |
| ||
| 3 |
| 3 |
∴∠FMN=∠PMC=60°,
∴∠FNM=90°,
而FM=PF-PM=6-2
| 3 |
在Rt△FMN中,∵∠F=30°,
∴MN=
| 1 |
| 2 |
| 3 |
∴FN=
| 3 |
| 3 |
∴△ABC与△DEF重叠部分的面积=S△FPH-S△FMN
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
=9(cm2).
故答案为9.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系.

练习册系列答案
相关题目
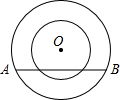 如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )
如图,以O为圆心的两个同心圆中,半径分别为3和5,若大圆的弦AB与小圆相交,则弦AB的长的取值范围是( )| A、8≤AB≤10 |
| B、8<AB<10 |
| C、8<AB≤10 |
| D、6≤AB≤10 |
 如图,△EFG≌△NMH,在△EFG中,FG是最长的边,在△NMH中,MH是最长的边,∠F和∠M是对应角,且EF=2.4cm,FH=1.9cm,HM=3.5cm.
如图,△EFG≌△NMH,在△EFG中,FG是最长的边,在△NMH中,MH是最长的边,∠F和∠M是对应角,且EF=2.4cm,FH=1.9cm,HM=3.5cm.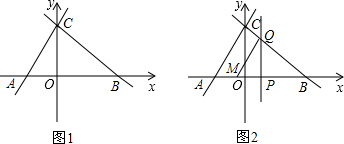
 如图,在△ABC中,点D在边AB上,∠ACD=∠ABC,AD=1,AB=3.求AC的长.
如图,在△ABC中,点D在边AB上,∠ACD=∠ABC,AD=1,AB=3.求AC的长. 如图,取一张长方形纸片,按图中所示的方法折叠一角,得到折痕PO,再折叠一角,得到折痕QO,如果两折痕的夹角∠POQ=70°,则∠AOB=
如图,取一张长方形纸片,按图中所示的方法折叠一角,得到折痕PO,再折叠一角,得到折痕QO,如果两折痕的夹角∠POQ=70°,则∠AOB= 【问题情境】
【问题情境】