题目内容
已知抛物线y=kx2-4x+1的图象与x轴有公共点,则k的取值范围是 .
考点:抛物线与x轴的交点
专题:
分析:先根据二次函数的定义得到k≠0,再根据抛物线与x轴的交点问题得到△=(-4)2-4k×1≥0,然后解不等式即可得到k的值.
解答:解:∵y=kx2-4x+1为二次函数,
∴k≠0,
∵二次函数y=kx2-4x+1的图象与x轴有公共点,
∴△=(-4)2-4k×1≥0,解得k≤4,
综上所述,k的取值范围是 k≤4且k≠0.
故答案是:k≤4且k≠0.
∴k≠0,
∵二次函数y=kx2-4x+1的图象与x轴有公共点,
∴△=(-4)2-4k×1≥0,解得k≤4,
综上所述,k的取值范围是 k≤4且k≠0.
故答案是:k≤4且k≠0.
点评:本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:当△=b2-4ac>0时,抛物线与x轴有2个交点;当△=b2-4ac=0时,抛物线与x轴有1个交点;当△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
 如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )
如图,∠A=80°,∠ADB=60°,∠DBC=20°,AD=3,DC=2.则AB=( )A、
| ||
B、
| ||
C、
| ||
| D、6 |
一次知识竞赛共有20道选择题,规定答对一道得5分,不做或错一题扣1分,结果某学生得分为88分,则他做对题数为( )
| A、16 | B、17 | C、18 | D、19 |
下列说法中正确的是( )
| A、若|a|=|b|,则a=b |
| B、若ac=bc,则a=b |
| C、若线段AC=BC,则点C是线段AB的中点 |
| D、过n边形的一个顶点有(n-3)条对角线 |
 如图,在△ABC中,点D在边AB上,∠ACD=∠ABC,AD=1,AB=3.求AC的长.
如图,在△ABC中,点D在边AB上,∠ACD=∠ABC,AD=1,AB=3.求AC的长. 【问题情境】
【问题情境】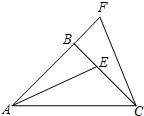 如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF