题目内容
18. 如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2$\sqrt{3}$,则AB的长为4.
如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2$\sqrt{3}$,则AB的长为4.
分析 由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,再由三角形ADF与三角形ECF全等,得出AF=EF,求出AG,由勾股定理求出AD,即可得出AB的长.
解答 解:∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,
又∵F为DC的中点,
∴DF=CF,
∴AD=DF=$\frac{1}{2}$DC=$\frac{1}{2}$AB,
∵DG⊥AE,
∴AG=FG,
∵平行四边形ABCD中,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中,$\left\{\begin{array}{l}{∠DAF=∠E}&{\;}\\{∠ADE=∠ECF}&{\;}\\{DF=CF}&{\;}\end{array}\right.$,
∴△ADF≌△ECF(AAS),
∴AF=EF=2$\sqrt{3}$,
∴AG=$\sqrt{3}$,
∴AD=$\sqrt{A{G}^{2}+D{G}^{2}}$=2,
∴AB=2AD=4;
故答案为:4.
点评 此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.计算(-3)×9的值是( )
| A. | 6 | B. | 27 | C. | -12 | D. | -27 |
13.已知菱形的周长为20,它的一条对角线长为6,则菱形的面积是( )
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
8. 如图,AB为⊙O的直径,C,D为⊙O上的两点,且CD⊥AB于点E,OF⊥AC于点F,连接BD.若∠D=30°,BC=1,则图中阴影部分的面积是( )
如图,AB为⊙O的直径,C,D为⊙O上的两点,且CD⊥AB于点E,OF⊥AC于点F,连接BD.若∠D=30°,BC=1,则图中阴影部分的面积是( )
 如图,AB为⊙O的直径,C,D为⊙O上的两点,且CD⊥AB于点E,OF⊥AC于点F,连接BD.若∠D=30°,BC=1,则图中阴影部分的面积是( )
如图,AB为⊙O的直径,C,D为⊙O上的两点,且CD⊥AB于点E,OF⊥AC于点F,连接BD.若∠D=30°,BC=1,则图中阴影部分的面积是( )| A. | $\frac{2\sqrt{3}}{3}$π | B. | $\frac{π}{3}$-$\frac{\sqrt{3}}{4}$ | C. | $\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$ | D. | π-$\sqrt{3}$ |
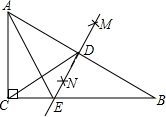 如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一).
如图,在△ABC中,∠ACB=90°,分别以点A、点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD、AE,请你依作图信息写一个正确的结论AE=BE(答案不唯一). 如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.
如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$. 如图,正方形ABCD边长是4,P是CD中点,Q是线段BC上一点,当CQ=4或1时,以由Q,C,P三点为顶点的三角形与△ADP相似.
如图,正方形ABCD边长是4,P是CD中点,Q是线段BC上一点,当CQ=4或1时,以由Q,C,P三点为顶点的三角形与△ADP相似.