题目内容
9. 如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.
如图,在Rt△ABC中,∠ABC=60°,$BC=\sqrt{3}$.①在BC、BA上分别截取BD、BE,使BD=BE;
②分别以D、E为圆心、以大于$\frac{1}{2}$DE的长为半径作圆弧,在∠ABC内两弧交于点O;
③作射线BO交AC于点F.
若点P是AB上的动点,则FP的最小值为1.
分析 利用基本作图得到BO平分∠ABC,则∠FBC=$\frac{1}{2}$∠ABC=30°,在Rt△BCF中利用含30度的直角三角形三边的关系得到CF=$\frac{\sqrt{3}}{3}$BC=1,然后根据角平分线的性质定理可得FP的最小值为1.
解答 解:由作法得BO平分∠ABC,
∵∠ABC=60°,
∴∠FBC=$\frac{1}{2}$∠ABC=30°,
在Rt△BCF中,CF=$\frac{\sqrt{3}}{3}$BC=$\frac{\sqrt{3}}{3}$×$\sqrt{3}$=1,
∴点F到AB的距离等于CF,即为1,
∴FP的最小值为1.
故答案为1.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了角平分线的性质.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
17.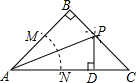 如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:
如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:
①AB=AD;②AP平分∠BAC;③△PDC的周长是10$\sqrt{2}$cm;④AN=ND,
正确的是( )
 如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:
如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:①AB=AD;②AP平分∠BAC;③△PDC的周长是10$\sqrt{2}$cm;④AN=ND,
正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
1.发展工业是强国之梦的重要举措,如图所示零件的左视图是( )


| A. |  | B. |  | C. |  | D. |  |
19.下列选项中,可以用来证明命题“若a2>b2,则a>b“是假命题的反例是( )
| A. | a=-2,b=1 | B. | a=3,b=-2 | C. | a=0,b=1 | D. | a=2,b=1 |


 如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2$\sqrt{3}$,则AB的长为4.
如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2$\sqrt{3}$,则AB的长为4.