题目内容
3. 正三角形ABC的边长为6,求它的中心角、半径和边心距.
正三角形ABC的边长为6,求它的中心角、半径和边心距.
分析 设正三角形ABC的中心为O连接OB,OC,作OD⊥BC于D,则∠BOC=120°,BD=CD=$\frac{1}{2}$BC=3,由等腰三角形的性质得出∠OBC=30°,得出OB=2OD,由三角函数求出OD=$\frac{\sqrt{3}}{3}$BD=$\sqrt{3}$,得出OB=2$\sqrt{3}$即可.
解答 解:设正三角形ABC的中心为O连接OB,OC,作OD⊥BC于D,如图所示: 则∠BOC=$\frac{360°}{3}$=120°,BD=CD=$\frac{1}{2}$BC=3,
则∠BOC=$\frac{360°}{3}$=120°,BD=CD=$\frac{1}{2}$BC=3,
∵OB=OC,
∴∠OBC=30°,
∴OB=2OD,OD=$\frac{\sqrt{3}}{3}$BD=$\sqrt{3}$,
∴OB=2$\sqrt{3}$;
即正三角形的中心角为120°,半径为2$\sqrt{3}$,边心距为$\sqrt{3}$.
点评 本题考查了正多边形和圆、正三角形的性质、含30°角的直角三角形的性质、三角函数;熟记正三角形的性质是解决问题的关键.

练习册系列答案
相关题目
12. 如图,在菱形ABCD中,∠BAD=120°,设∠ABD=α,则下列等式正确的是( )
如图,在菱形ABCD中,∠BAD=120°,设∠ABD=α,则下列等式正确的是( )
 如图,在菱形ABCD中,∠BAD=120°,设∠ABD=α,则下列等式正确的是( )
如图,在菱形ABCD中,∠BAD=120°,设∠ABD=α,则下列等式正确的是( )| A. | sinα=$\frac{\sqrt{3}}{2}$ | B. | tanα=$\sqrt{3}$ | C. | cosα=$\frac{1}{2}$ | D. | cosα=$\frac{\sqrt{3}}{2}$ |
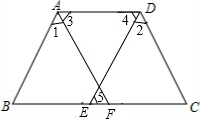 如图,已知∠1=∠2,∠4=∠5,∠3=∠C,求证:AB∥DE.
如图,已知∠1=∠2,∠4=∠5,∠3=∠C,求证:AB∥DE. 由于过度砍伐森林和破坏植被,我国某些地区经常受到沙尘暴的侵袭,如图,某日A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向移动,移动速度为20km/h,距沙尘暴中心300km的范围内将受到影响,问A市是否会受到这次沙尘暴的影响?影响时间多长?
由于过度砍伐森林和破坏植被,我国某些地区经常受到沙尘暴的侵袭,如图,某日A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向移动,移动速度为20km/h,距沙尘暴中心300km的范围内将受到影响,问A市是否会受到这次沙尘暴的影响?影响时间多长? 如图,AB是⊙O的弦,OD⊥OB,交AB于E,且AD=ED.求证:AD是⊙O的切线.
如图,AB是⊙O的弦,OD⊥OB,交AB于E,且AD=ED.求证:AD是⊙O的切线. 如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.
如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF. 如图,AC=10,∠BAC=30°,∠ABC=45°,将△ABC绕AM旋转一周,可得到一个立体图形,求该立体图形的表面积.
如图,AC=10,∠BAC=30°,∠ABC=45°,将△ABC绕AM旋转一周,可得到一个立体图形,求该立体图形的表面积. 如图,抛物线y=ax2经过点A、B,x轴上两点C(-2,0),D(4,0).四边形ABDC是菱形,求抛物线的表达式.
如图,抛物线y=ax2经过点A、B,x轴上两点C(-2,0),D(4,0).四边形ABDC是菱形,求抛物线的表达式.