题目内容
18. 如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.
如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.
分析 根据三角形中位线的性质得到FG=$\frac{1}{2}$AD,EG=$\frac{1}{2}$BC,由AD=BC,于是得到FG=GE,根据等腰三角形的性质即可得到结论.
解答 证明:∵E,F,G分别是AB,CD,AC的中点,
∴FG=$\frac{1}{2}$AD,EG=$\frac{1}{2}$BC,
∵AD=BC,
∴FG=GE,
∵H是EF的中点,
∴GH⊥EF.
点评 本题考查了三角形的中位线的性质,等腰三角形的判定和性质,少了掌握三角形的中位线的性质是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 画出以下几何体的三视图.
画出以下几何体的三视图.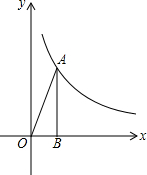 如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2.
如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2. 如图:计算下面各个图形的表面积与体积.
如图:计算下面各个图形的表面积与体积. 正三角形ABC的边长为6,求它的中心角、半径和边心距.
正三角形ABC的边长为6,求它的中心角、半径和边心距. 如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求:
如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求: 如图,AD∥BE,BD∥CE.
如图,AD∥BE,BD∥CE.