题目内容
15. 如图,抛物线y=ax2经过点A、B,x轴上两点C(-2,0),D(4,0).四边形ABDC是菱形,求抛物线的表达式.
如图,抛物线y=ax2经过点A、B,x轴上两点C(-2,0),D(4,0).四边形ABDC是菱形,求抛物线的表达式.
分析 由点的坐标得出OC=2,OD=4,得出CD=6,由菱形的性质得出AB∥CD,AB=CD=BD=6,得出AM=BM=3,作BN⊥CD于N,则∠BND=90°,ON=BM=3,DN=1,由勾股定理求出BN,得出点B的坐标,代入y=ax2求出a的值即可.
解答 解:如图所示:
∵C(-2,0),D(4,0),
∴OC=2,OD=4,
∴CD=6,
∵四边形ABDC是菱形,
∴AB∥CD,AB=CD=BD=6,
∴AM=BM=3,
作BN⊥CD于N,
则∠BND=90°,ON=BM=3,
∴DN=1,
∴BN=$\sqrt{{6}^{2}-{1}^{2}}$=$\sqrt{35}$,
∴点B的坐标为(3,-$\sqrt{35}$),
把B(3,-$\sqrt{35}$)代入y=ax2得:9a=-$\sqrt{35}$,
解得:a=-$\frac{\sqrt{35}}{9}$,
∴抛物线的表达式为y=-$\frac{\sqrt{35}}{9}$x2.
点评 本题考查了菱形的性质、待定系数法求抛物线的解析式、坐标与图形性质、勾股定理;熟练掌握菱形的性质,求出点B的坐标是解决问题的关键.

练习册系列答案
相关题目
5.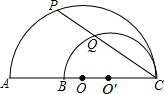 如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
 如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )| A. | 5cm | B. | 5$\sqrt{3}$cm | C. | 6cm | D. | 8cm |
4.下列语句中表述正确的是( )
| A. | 延长射线OC | B. | 射线BA与射线AB是同一条射线 | ||
| C. | 直线AB=直线BC | D. | 延长线段AB至点C,使得线段BC=AB |
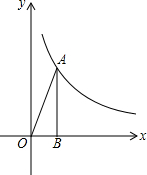 如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2.
如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2. 正三角形ABC的边长为6,求它的中心角、半径和边心距.
正三角形ABC的边长为6,求它的中心角、半径和边心距. 如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求:
如图,拦水坝的横断面为梯形ABCD,坝高23米.坝面宽BC=6米.根据条件求: 八(二)班举行元旦文艺晚会,桌子摆成两条直线(如图中所示的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的小花先拿桔子再拿糖果,然后送给D处的小红,最后回到C处.请你帮助她设计一条行走路线,使其所走的总路程最短(尺规作图,并写出作法,不需说明理由)
八(二)班举行元旦文艺晚会,桌子摆成两条直线(如图中所示的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的小花先拿桔子再拿糖果,然后送给D处的小红,最后回到C处.请你帮助她设计一条行走路线,使其所走的总路程最短(尺规作图,并写出作法,不需说明理由) 如图,AD∥BE,BD∥CE.
如图,AD∥BE,BD∥CE.