题目内容
 如图,正方形ABCD中,E为AB中点,EF⊥DE且BF平分∠CBM,求证:DE=EF.
如图,正方形ABCD中,E为AB中点,EF⊥DE且BF平分∠CBM,求证:DE=EF.考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:作FG⊥AM于G,根据BF平分∠CBM,推得△FGB是等腰直角三角形,推出FG=BG,然后根据三角形相似推出EG=2FG,从而推出FG=EB,进而推出FG=AE,最后根据AAS证得△ADE≌△GEF,即可证得结论;
解答: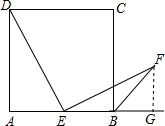 证明:作FG⊥AM于G,
证明:作FG⊥AM于G,
∵BF平分∠CBM,
∴三角形BFG是等腰直角三角形,
∴FG=BG,
∵EF⊥DE,
∴∠AED+∠FEB=90°,
∵∠AED+∠ADE=90°,
∴∠ADE=∠FEB,
∵∠A=∠FGE=90°
∴△ADE∽△GEF,
∴
=
=
,
∴EG=2FG,
∴FG=BE,
∴FG=AE,
在△ADE与△GEF中,
,
∴△ADE≌△GEF(AAS),
∴DE=EF.
 证明:作FG⊥AM于G,
证明:作FG⊥AM于G,∵BF平分∠CBM,
∴三角形BFG是等腰直角三角形,
∴FG=BG,
∵EF⊥DE,
∴∠AED+∠FEB=90°,
∵∠AED+∠ADE=90°,
∴∠ADE=∠FEB,
∵∠A=∠FGE=90°
∴△ADE∽△GEF,
∴
| AE |
| AD |
| FG |
| EG |
| 1 |
| 2 |
∴EG=2FG,
∴FG=BE,
∴FG=AE,
在△ADE与△GEF中,
|
∴△ADE≌△GEF(AAS),
∴DE=EF.
点评:本题考查了正方形的性质,三角形相似的判定和性质,三角形全等的判定和性质,等腰直角三角形的性质等,作FG⊥AM构建全等三角形是本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知半⊙O的直径AB=12,AD、BC、CD是⊙O的切线,E是半⊙O上的动切点,AD=x,BC=y.
如图,已知半⊙O的直径AB=12,AD、BC、CD是⊙O的切线,E是半⊙O上的动切点,AD=x,BC=y. 小明在画函数y=|x|的图象时,得到了如图甲所示的图象.他发现这个图象好像是把函数y=x的图象x轴下方的部分翻折到x轴上方(如图乙).于是他得出这样的结论:y=|kx+b|的图象都可以这样做,你认为他的结论正确吗?能由y=kx+b的图象得到y=|kx+b|的图象吗?
小明在画函数y=|x|的图象时,得到了如图甲所示的图象.他发现这个图象好像是把函数y=x的图象x轴下方的部分翻折到x轴上方(如图乙).于是他得出这样的结论:y=|kx+b|的图象都可以这样做,你认为他的结论正确吗?能由y=kx+b的图象得到y=|kx+b|的图象吗?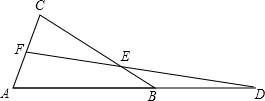 如图,△ABC中,D为AB延长线上一点,E、F分别为BC、AC上一点,已知AF=EB,求证:BC•ED=AC•DF.
如图,△ABC中,D为AB延长线上一点,E、F分别为BC、AC上一点,已知AF=EB,求证:BC•ED=AC•DF.