题目内容
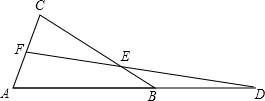如图，△ABC中，D为AB延长线上一点，E、F分别为BC、AC上一点，已知AF=EB，求证：BC•ED=AC•DF．考点：相似三角形的判定与性质
专题：证明题
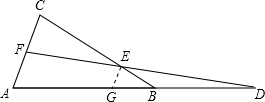
分析：过点E作EG∥AC交AB于G．先由EG∥AF，得出△DAF∽△DGE，根据相似三角形对应边成比例得到
=
，将AF=EB代入，得到
=
①，再由EG∥AC，得出△BAC∽△BGE，根据相似三角形对应边成比例得到
=
，即
=
②，比较①②，得
=
，根据比例的基本性质即可证明BC•ED=AC•DF．
| DF |
| DE |
| AF |
| GE |
| DF |
| DE |
| EB |
| GE |
| BC |
| BE |
| AC |
| GE |
| BC |
| AC |
| EB |
| GE |
| DF |
| DE |
| BC |
| AC |
解答：证明：如图，过点E作EG∥AC交AB于G．
∵EG∥AF，
∴△DAF∽△DGE，
∴
=
，
∵AF=EB，
∴
=
①．
∵EG∥AC，
∴△BAC∽△BGE，
∴
=
，
∴
=
②．
比较①②，得
=
，
∴BC•ED=AC•DF．
∵EG∥AF，
∴△DAF∽△DGE，
∴
| DF |
| DE |
| AF |
| GE |
∵AF=EB，
∴| DF |
| DE |
| EB |
| GE |
∵EG∥AC，
∴△BAC∽△BGE，
∴
| BC |
| BE |
| AC |
| GE |
∴
| BC |
| AC |
| EB |
| GE |
比较①②，得
| DF |
| DE |
| BC |
| AC |
∴BC•ED=AC•DF．
点评：本题考查了相似三角形的判定与性质，比例的性质，难度适中．准确作出辅助线是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，正方形ABCD中，E为AB中点，EF⊥DE且BF平分∠CBM，求证：DE=EF．