题目内容
若a是关于x的方程x2-2013x+1=0的一个根,求a2-2012a+
的值.
| 2013 |
| a2-1 |
考点:一元二次方程的解
专题:
分析:根据一元二次方程的解的定义得到a2-2013a+1=0,变形得a2=2013a-1,把a2=2013a-1代入所求的代数式合并得到a-1+
,然后通分后再次利用整体代入的方法计算即可.
| 1 |
| a |
解答:解:∵a是方程x2-2013x+1=0的一个解,
∴a2-2013a+1=0,
∴a2=2013a-1,
∴原式=2013a-1-2012a+
=a-1+
=
-1
=
-1
=2013-1
=2012.
∴a2-2013a+1=0,
∴a2=2013a-1,
∴原式=2013a-1-2012a+
| 2013 |
| 2013a-1+1 |
=a-1+
| 1 |
| a |
=
| a2+1 |
| a |
=
| 2013a-1+1 |
| a |
=2013-1
=2012.
点评:本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
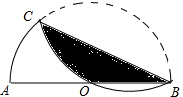 已知半径为6的半圆,沿BC对折,
已知半径为6的半圆,沿BC对折, |
| BC |
| A、6π | ||
B、4
| ||
C、3
| ||
D、2
|
 如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移得到△OBD.连结AD,交OC于点E,求点E坐标.
如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移得到△OBD.连结AD,交OC于点E,求点E坐标. 如图,正方形ABCD中,E为AB中点,EF⊥DE且BF平分∠CBM,求证:DE=EF.
如图,正方形ABCD中,E为AB中点,EF⊥DE且BF平分∠CBM,求证:DE=EF. 如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜.
如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜.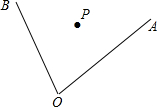 根据语句作图,并回答问题.如图,∠AOB内有一点P.
根据语句作图,并回答问题.如图,∠AOB内有一点P.