题目内容
11.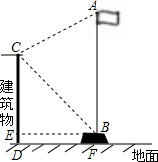 如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
分析 作CG⊥AB于点G,构成两个直角三角形.运用三角函数定义分别求出AG和BG,即可解答.
解答  解:作CG⊥AB于点G.
解:作CG⊥AB于点G.
根据题意可得:在△GBC中,有BG=GC×tan45°=9.
在△AGC中,有AG=FC×tan30°=3$\sqrt{3}$.
∴AB=9+3$\sqrt{3}$.
∵BF=0.6米,
∴点A离地面的高度=0.6+9+3$\sqrt{3}$=(9.6+3$\sqrt{3}$)m=14.8m.
即旗杆顶点A离地面的高度为14.8m.
点评 本题考查俯角、仰角的定义,要求学生能借助其关系构造直角三角形并解直角三角形.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1.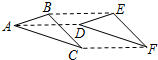 如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
 如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )
如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是( )| A. | BC∥EF | B. | AD=BE | C. | BE∥CF | D. | AC=EF |
2.下列几组数中,能作为直角三角形三边长度的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 6,8,11 | D. | 5,12,13 |
19.要使分式$\frac{x-3}{{{x^2}+6x+9}}$有意义,那么x的取值范围是( )
| A. | x≠3 | B. | x≠3且x≠-3 | C. | x≠0且x≠-3 | D. | x≠-3 |
3.若A(1,y1),B(2,y2)两点都在反比例函数y=$\frac{1}{x}$的图象上,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
 如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.
如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.