题目内容
3.若A(1,y1),B(2,y2)两点都在反比例函数y=$\frac{1}{x}$的图象上,则y1与y2的大小关系是( )| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 无法确定 |
分析 根据反比例函数图象上点的坐标特征结合点A、B的横坐标,求出y1、y2的值,二者进行比较即可得出结论.
解答 解:∵A(1,y1),B(2,y2)两点都在反比例函数y=$\frac{1}{x}$的图象上,
∴1•y1=1,2•y2=1,
解得:y1=1,y2=$\frac{1}{2}$,
∵1>$\frac{1}{2}$,
∴y1>y2.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征,解题的关键是根据反比例函数图象上点的坐标特征求出y1、y2的值.本题属于基础题,难度不大,解决该题型题目时,结合点的横坐标,利用反比例函数图象上点的坐标特征求出点的纵坐标是关键.

练习册系列答案
相关题目
13.已知菱形ABCD的对角线AC,BD的长分别为6和8,则该菱形面积是( )
| A. | 14 | B. | 24 | C. | 30 | D. | 48 |
18. 如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )
如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )
 如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )
如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )| A. | 25° | B. | 35° | C. | 50° | D. | 60° |
14.数据4,2,6的平均数和方差分别是( )
| A. | 2,$\frac{8}{3}$ | B. | 2,$\frac{4}{3}$ | C. | 4,$\frac{8}{3}$ | D. | 4,$\frac{4}{3}$ |
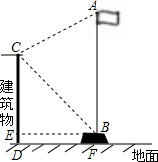 如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).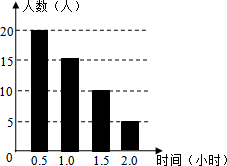 某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.
某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.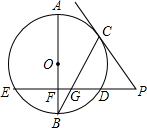 如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.
如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.