题目内容
1. 如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.
如图,二次函数$y=\frac{1}{2}{(x-3)^2}-1$的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,顶点为D.(1)求点A,B,D的坐标;
(2)连接CD,过原点O作OE⊥CD,垂足为H,OE与该图象的对称轴交于点E,连接AE,AD,求∠DAE的大小;
(3)设点E关于点D的对称点为F,分别以E,F为圆心,1为半径作两个圆,该二次函数的图象上是否存在一点P,使得过P向两个圆各作一条切线PM,PN(M,N为切点),且PM,PN刚好可以作为一个斜边为4的直角三角形的两条直角边?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)令y=0,即可求出点A、B坐标,根据顶点式可以知道点D坐标.
(2)先求出直线CD解析式,根据OE⊥CD求出直线OE解析式,再求出点E坐标,利用两点间距离公式求出线段AE2,AD2,DE2,由勾股定理的逆定理证明△EAD是直角三角形即可解决问题.
(3)存在.设点P为(m,n),求出PM2,PN2,根据PM2+PN2=42,列出方程即可解决问题.
解答 解:(1)令y=0,则$\frac{1}{2}$(x-3)2-1=0,解得x=3$±\sqrt{2}$,
∴点A坐标(3-$\sqrt{2}$,0),点B坐标(3+$\sqrt{2}$,0),
令x=0则y=$\frac{7}{2}$,
∴点C坐标(0,$\frac{7}{2}$),顶点D坐标(3,-1).
(2)设直线CD解析式为y=kx+b,
则$\left\{\begin{array}{l}{3k+b=-1}\\{b=\frac{7}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{7}{2}}\end{array}\right.$,
∴直线CD解析式为y=-$\frac{3}{2}$x+$\frac{7}{2}$,
∵OE⊥CD,
∴直线OE解析式为y=$\frac{2}{3}$x,
∴x=3时,y=2,
∴点E坐标(3,2),
∴AE2=($\sqrt{2}$)2+22=6,AD2=($\sqrt{2}$)2+12=3,DE2=32=9,
∴AE2+AD2=DE2,
∴∠EAD=90°.
(3)存在.
理由:由题意E(3,2),F(3,-4),设点P为(m,n),
∵点P在抛物线上,
∴n=$\frac{1}{2}$(m-3)2-1 ①
∴PM2=PE2-12=(m-3)2+(n-2)2-1,PN2=PF2-12=(m-3)2+(n+4)2-1,
∵PM2+PN2=42,
∴(m-3)2+(n-2)2-1+(m-3)2+(n+4)2-1=42,
整理得到(m-3)2+(n+1)2=0 ②
由①②得到m=3,n=-1,
∴点P坐标(3,-1).
点评 本题考查二次函数综合题、一次函数.两点间距离公式、勾股定理、非负数的性质等知识,解题的关键是熟练掌握求抛物线与坐标轴的交点,学会理由参数解决问题,本题有一定的代数技巧,巧用非负数的性质这个突破口,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. |  | B. |  | C. |  | D. |  |
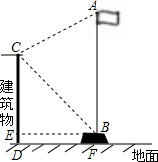 如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°,旗杆底部B点的俯角为45°,若旗杆底部B点到该建筑物的水平距离BE=9米,旗杆台阶的高BF=0.6米,A、B、F在同一直线上,求旗杆顶部A离地面的高度AF(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).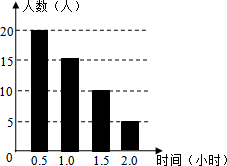 某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.
某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.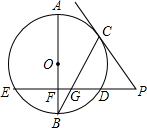 如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.
如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.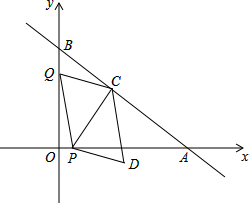 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(8,0),B(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造?PQCD,设点P运动的时间为t秒.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(8,0),B(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造?PQCD,设点P运动的时间为t秒.