题目内容
19．要使分式$\frac{x-3}{{{x^2}+6x+9}}$有意义，那么x的取值范围是（ ）| A． | x≠3 | B． | x≠3且x≠-3 | C． | x≠0且x≠-3 | D． | x≠-3 |
分析 根据分式有意义的条件列出关于x的不等式，求解即可．
解答 解：∵x2+6x+9≠0，
∴（x+3）2≠0，
∴x+3≠0，
∴x≠-3，
∴分式$\frac{x-3}{{{x^2}+6x+9}}$有意义，x的取值范围x≠-3，
故选D．
点评 本题考查了分式有意义的条件：分母不为0，掌握不等式的解法是解题的关键．
练习册系列答案
相关题目
9．如图所示，长为2宽为1的矩形和边长为3的正方形在同一水平线上，矩形沿该水平线从左向右匀速穿过正方形；设穿过的时间为t，正方形除去矩形面积为S（阴影部分），则S与t的大致图象为（ ）
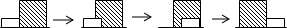
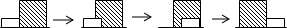
| A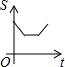． |  | B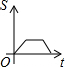． |  | C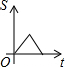． |  | D． |  |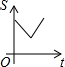
10．如图图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．阅读对人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科文组织确定为“世界读书日”．某校本学年开展了读书活动，在这次活动中，八年级（1）班40名学生读书册数的情况如表：
根据表中的数据，求：
（1）该班学生读书册数的平均数；
（2）该班学生读书册数的中位数．
| 读书册数 | 4 | 5 | 6 | 7 | 8 |
| 人数（人） | 6 | 4 | 10 | 12 | 8 |
（1）该班学生读书册数的平均数；
（2）该班学生读书册数的中位数．
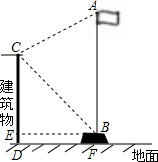如图，张聪同学在学校某建筑物C点处测得旗杆顶部A的仰角为30°，旗杆底部B点的俯角为45°，若旗杆底部B点到该建筑物的水平距离BE=9米，旗杆台阶的高BF=0.6米，A、B、F在同一直线上，求旗杆顶部A离地面的高度AF（结果精确到0.1米，参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．
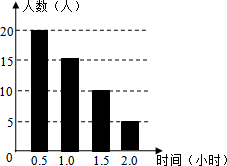某校为了解学生课外阅读情况，随机调查了50名学生各自平均每天的课外阅读时间，并绘制成条形图，据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时．
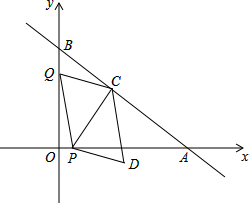如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（8，0），B（0，6），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点Q从点B出发，沿射线BO方向以每秒2个单位的速度运动，过点P作PC⊥AB于点C，连接PQ，CQ，以PQ，CQ为邻边构造?PQCD，设点P运动的时间为t秒．