题目内容
8. 如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{AE}{EC}$=$\frac{BF}{FC}$ | C. | $\frac{AD}{BD}$=$\frac{BF}{FC}$ | D. | $\frac{BD}{AD}$=$\frac{BF}{FC}$ |
分析 根据平行线分线段长比例定理可对A、B进行判断;利用A、B的结论可得到$\frac{AD}{DB}$=$\frac{BF}{FC}$,可对C、D进行判断.
解答 解:A、∵DE∥BC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,所以A选项的等式成立;
B、∵EF∥AB,
∴$\frac{AE}{EC}$=$\frac{BF}{FC}$,所以B选项的等式成立;
C、∵DE∥BC,
∴$\frac{AD}{DB}$=$\frac{AE}{EC}$,
而$\frac{AE}{EC}$=$\frac{BF}{FC}$,
∴$\frac{AD}{DB}$=$\frac{BF}{FC}$,所以C选项的等式成立;
D、∵$\frac{AD}{DB}$=$\frac{BF}{FC}$,
∴$\frac{BD}{AD}$=$\frac{FC}{BF}$,所以D选项的等式不成立.
故选D.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.

练习册系列答案
相关题目
19.若要从二次函数y=3x2的图象得到二次函数y=3(x+2)2-1的图象,则二次函数y=3x2的图象必须( )
| A. | 上移1个单位,右移2个单位 | B. | 下移1个单位,右移2个单位 | ||
| C. | 下移1个单位,左移2个单位 | D. | 上移2个单位,右移1个单位 |
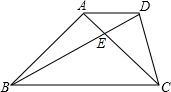 如图,已知梯形ABCD,AD∥BC,BD=BC,AB=AC,∠BAC=90°.求:sin∠DBC.
如图,已知梯形ABCD,AD∥BC,BD=BC,AB=AC,∠BAC=90°.求:sin∠DBC. 如图,已知△ABC是等边三角形,将△ABC绕点A逆时针方向旋转20°,得到△ADE,BD和EC所在直线相交于点O.求∠BOE的度数.
如图,已知△ABC是等边三角形,将△ABC绕点A逆时针方向旋转20°,得到△ADE,BD和EC所在直线相交于点O.求∠BOE的度数.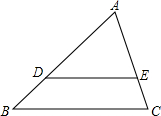 如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.