题目内容
13.已知a、b、c是△ABC的三边长,且$\frac{a}{5}$=$\frac{b}{4}$=$\frac{c}{6}$≠0,求:(1)$\frac{2a+b}{3c}$的值.
(2)若△ABC的周长为90,求各边的长.
分析 (1)设$\frac{a}{5}$=$\frac{b}{4}$=$\frac{c}{6}$=k,易得a=5k,b=4k,c=6k,然后把它们分别代入$\frac{2a+b}{3c}$中,再进行分式的运算即可;
(2)根据三角形周长定义得到5k+4k+6k=90,解关于k的方程求出k,然后计算5k、4k和6k即可.
解答 解:(1)设$\frac{a}{5}$=$\frac{b}{4}$=$\frac{c}{6}$=k,则a=5k,b=4k,c=6k,
所以$\frac{2a+b}{3c}$=$\frac{10k+4k}{18k}$=$\frac{7}{9}$;
(2)5k+4k+6k=90,解得k=6,
所以a=30,b=24,c=36.
点评 本题考查了比例线段:对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,如 a:b=c:d(即ad=bc),我们就说这四条线段是成比例线段,简称比例线段.

练习册系列答案
相关题目
3.一元二次方程(x-4)2=2x-3化为一般式是( )
| A. | x2-10x+13=0 | B. | x2-10x+19=0 | C. | x2-6x+13=0 | D. | x2-6x+19=0 |
8. 如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
 如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{AE}{EC}$=$\frac{BF}{FC}$ | C. | $\frac{AD}{BD}$=$\frac{BF}{FC}$ | D. | $\frac{BD}{AD}$=$\frac{BF}{FC}$ |
5.下列各题的计算,正确的是( )
| A. | (a7)2=a9 | B. | a7•a2=a14 | ||
| C. | 2a2+3a2=6a5 | D. | (-0.5)2010×22011=2 |
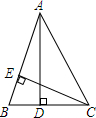 如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.
如图,在△ABC中,AD,CE是△ABC的高,找出图中的一组比例线段,并说明理由.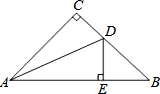 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DBE的周长8.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB于E.若AB=8,则△DBE的周长8.