题目内容
17.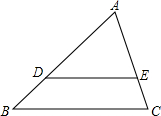 如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.(1)如果AD=3.2cm,DB=1.2cm,AE=2.4cm,那么EC的长是多少?
(2)如果AB=5cm,AD=3cm,AC=4cm,哪么EC的长是多少?
分析 (1)根据平行线分线段成比例定理得到$\frac{3.2}{1.2}$=$\frac{2.4}{EC}$,然后利用比例性质求CE;
(2)根据平行线分线段成比例定理得$\frac{3}{5-3}$=$\frac{4-EC}{EC}$,然后利用比例性质求CE.
解答 解2:(1)∵DE∥BC,
∴$\frac{AD}{DB}$=$\frac{AE}{EC}$,即$\frac{3.2}{1.2}$=$\frac{2.4}{EC}$,
∴EC=0.9(cm);
(2)∵DE∥BC,
∴$\frac{AD}{DB}$=$\frac{AE}{EC}$,即$\frac{3}{5-3}$=$\frac{4-EC}{EC}$,
∴EC=1.6(cm).
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了比例的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
 如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{AE}{EC}$=$\frac{BF}{FC}$ | C. | $\frac{AD}{BD}$=$\frac{BF}{FC}$ | D. | $\frac{BD}{AD}$=$\frac{BF}{FC}$ |
5.下列各题的计算,正确的是( )
| A. | (a7)2=a9 | B. | a7•a2=a14 | ||
| C. | 2a2+3a2=6a5 | D. | (-0.5)2010×22011=2 |
9.某市七天的空气质量指数分别是:28,45,28,45,45,30,53,这组数据的众数是( )
| A. | 28 | B. | 30 | C. | 45 | D. | 53 |
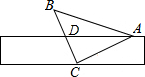 如图,将一个有45°角的三角板的直角顶点C在一张宽为1cm的纸带边沿上,另一个顶点A放在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则tan∠DAB=2-$\sqrt{3}$.
如图,将一个有45°角的三角板的直角顶点C在一张宽为1cm的纸带边沿上,另一个顶点A放在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则tan∠DAB=2-$\sqrt{3}$.