题目内容
18.已知直线l的解析式为y=x-2和点A(0,-2),B(-1,-3),试判断直线l上是否存在一点P,使P,A,B三点在同一个圆上?为什么?分析 由直线l的解析式得出A(0,-2),B(-1,-3)都在直线l上,由不在同一直线上的三个点确定一个圆,即可得出结论.
解答 解:直线l上不存在一点P,使P,A,B三点在同一个圆上.理由如下:
∵对于直线y=x-2,
当x=0时,y=-2;当x=-1时,y=-3;
∴A(0,-2),B(-1,-3)都在直线l上,
∵不在同一直线上的三个点确定一个圆,
∴直线l上不存在一点P,使P,A,B三点在同一个圆上.
点评 本题考查了三点共圆的条件、坐标与图形性质、直线上点的坐标特征;熟练掌握不在同一直线上的三个点确定一个圆是解决问题的关键;本题综合性强,难度适中.

练习册系列答案
相关题目
3.一元二次方程(x-4)2=2x-3化为一般式是( )
| A. | x2-10x+13=0 | B. | x2-10x+19=0 | C. | x2-6x+13=0 | D. | x2-6x+19=0 |
10.计算-5+4的结果是( )
| A. | -9 | B. | 1 | C. | -1 | D. | 不确定 |
8. 如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
 如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )
如图,D、E、F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式不成立的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{AE}{EC}$=$\frac{BF}{FC}$ | C. | $\frac{AD}{BD}$=$\frac{BF}{FC}$ | D. | $\frac{BD}{AD}$=$\frac{BF}{FC}$ |
 如图,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=100π,S2=80π,则S3=20π.
如图,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=100π,S2=80π,则S3=20π. 在△ABC中,AB=AC,BE平分∠ABC,DE∥BC,求证:DE=EC.
在△ABC中,AB=AC,BE平分∠ABC,DE∥BC,求证:DE=EC.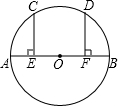 如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB,DF⊥AB,垂足分别为E、F,且AE=BF,$\widehat{AC}$与$\widehat{BD}$相等吗?为什么?
如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB,DF⊥AB,垂足分别为E、F,且AE=BF,$\widehat{AC}$与$\widehat{BD}$相等吗?为什么?