题目内容
13.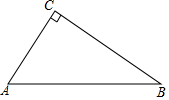 如图,已知△CAB,∠ACB=90°.
如图,已知△CAB,∠ACB=90°.(1)请用直尺和圆规过点C作一条裁剪线,使其将△ABC分成两个相似的三角形.(保留作图痕迹,不写作法)
(2)若CA=3,CB=4,则(1)中作的裁剪线的长为$\frac{12}{5}$.
分析 (1)过点C作AB的垂线段即可得;
(2)根据勾股定理求得AB=5,利用直角三角形的面积求解可得.
解答 解:(1)如图所示,CD即为所求;
(2)在Rt△ABC中,∵AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
则$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×CD,
解得:CD=$\frac{12}{5}$,
故答案为:$\frac{12}{5}$.
点评 本题主要考查相似变换的作图,熟练掌握相似三角形的判定和过直线外一点作已知直线的垂线是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
4.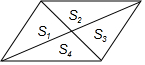 如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )
如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )
 如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )
如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )| A. | S1<S2<S3<S4 | B. | S1=S2=S3=S4 | C. | S1+S2>S3+S4 | D. | S1=S3<S2=S4 |
1.有五张不透明的卡片,正面的数分别写有3.101001000,$\frac{7}{3}$,π,$\sqrt{6}$,3.$\stackrel{••}{12}$,除正面的数不同外,其余都相同,将它们背面朝上洗匀后,从中随机抽取一张卡片,抽到写有有理数卡片的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
3.若一个多边形的每个内角都为108°,则它的边数为( )
| A. | 5 | B. | 8 | C. | 6 | D. | 10 |
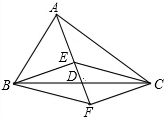 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).