题目内容
2.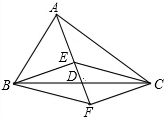 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).
分析 根据点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,即可证明四边形BECF是平行四边形,然后根据菱形的判定定理即可作出判断.
解答 解:∵BD=CD,DE=DF,
∴四边形BECF是平行四边形,
①BE⊥EC时,四边形BECF是矩形,不一定是菱形;
②AB=AC时,∵D是BC的中点,
∴AF是BC的中垂线,
∴BE=CE,
∴平行四边形BECF是菱形.
③四边形BECF是平行四边形,则BF∥EC一定成立,故不一定是菱形;
故答案是:②.
点评 本题考查了菱形的判定方法,菱形的判别常用三种方法:
①定义;②四边相等;③对角线互相垂直平分.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
17.下列运算中错误的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=2 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | (-$\sqrt{3}$)2=3 |
7.一长方形的长为8,对角线长为10,则它的面积为( )
| A. | 48 | B. | 40 | C. | 30 | D. | 12 |
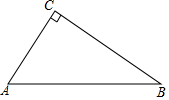 如图,已知△CAB,∠ACB=90°.
如图,已知△CAB,∠ACB=90°.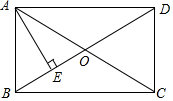 如图,矩形ABCD中,对角线AC、BD相交于点O,且AC=8,AE垂直平分OB于点E,则矩形ABCD的面积为16$\sqrt{3}$.
如图,矩形ABCD中,对角线AC、BD相交于点O,且AC=8,AE垂直平分OB于点E,则矩形ABCD的面积为16$\sqrt{3}$.
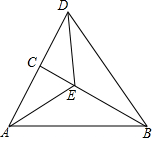 如图,已知在△ABC中,∠ACB=90°,∠BAC=60°,AE是∠BAC的平分线,延长AC至点D,使CD=AC.
如图,已知在△ABC中,∠ACB=90°,∠BAC=60°,AE是∠BAC的平分线,延长AC至点D,使CD=AC.