题目内容
5.在“幸运52”栏目中,游戏规则是:在12个商标牌中,有4个商标牌的背面注明了一定的奖金,其余商标牌的背面是一张“笑脸”,若翻到“笑脸”就不获奖,参与这个游戏的观众有三次翻牌的机会,且翻过的牌不能再翻,有一位观众已翻牌两次,两次都没获奖,则这位观众第三次翻牌获奖的概率是$\frac{2}{5}$.分析 根据题意,用背面注明了一定的奖金的商标牌的数量除以12-2,求出这位观众第三次翻牌获奖的概率是多少即可.
解答 解:4÷(12-2)
=4÷10
=$\frac{2}{5}$
答:这位观众第三次翻牌获奖的概率是$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 此题主要考查了概率的意义和应用,要熟练掌握,解答此题的关键是要明确:一般地,在大量重复实验中,如果事件A发生的频率mn会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率.

练习册系列答案
相关题目
17.下列运算中错误的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=2 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | (-$\sqrt{3}$)2=3 |
 如图是小芹3月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是1.5小时.
如图是小芹3月1日-7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是1.5小时. 将一副直角三角尺如图放置(其中∠A=60°,∠F=45°),点E在AC上,ED∥BC,则∠AEF的度数是165°.
将一副直角三角尺如图放置(其中∠A=60°,∠F=45°),点E在AC上,ED∥BC,则∠AEF的度数是165°.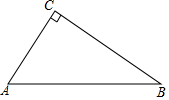 如图,已知△CAB,∠ACB=90°.
如图,已知△CAB,∠ACB=90°. 如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD
如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD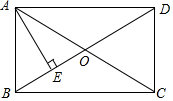 如图,矩形ABCD中,对角线AC、BD相交于点O,且AC=8,AE垂直平分OB于点E,则矩形ABCD的面积为16$\sqrt{3}$.
如图,矩形ABCD中,对角线AC、BD相交于点O,且AC=8,AE垂直平分OB于点E,则矩形ABCD的面积为16$\sqrt{3}$.