题目内容
13.已知,x,y,z为三个非负实数,且满足$\left\{\begin{array}{l}{3x+2y+z=5}\\{2x+y-3z=1}\end{array}\right.$,设S=3x+y-7z,则S的最大值是( )| A. | -$\frac{1}{11}$ | B. | $\frac{1}{11}$ | C. | -$\frac{5}{7}$ | D. | -$\frac{7}{5}$ |
分析 把方程组看作关于x、y的二元一次方程组,解得x=7z-3,y=-11z+7,则用z表示出S得到S=3z-2,再利用x,y,z为三个非负实数得到$\frac{3}{7}$≤z≤$\frac{7}{11}$,然后利用一次函数的性质求S的最大值.
解答 解:$\left\{\begin{array}{l}{3x+2y+z=5①}\\{2x+y-3z=1②}\end{array}\right.$,
②×2-①得x-7z=-3,所以x=7z-3,
把x=7z-3代入②得14z-6+y-3z=1,所以y=-11z+7,
所以S=3(7z-3)+(-11z+7)-7z=3z-2,
因为$\left\{\begin{array}{l}{x≥0}\\{7z-3≥0}\\{-11z+7≥0}\end{array}\right.$,
所以$\frac{3}{7}$≤z≤$\frac{7}{11}$,
当z=$\frac{7}{11}$时,S有最大值,最大值为3×$\frac{7}{11}$-2=-$\frac{1}{11}$.
故选A.
点评 本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.也考查了解三元一次方程组.

练习册系列答案
相关题目
 如图,已知线段及∠M,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠M,∠C=2∠M(保留作图痕迹,不写作法)
如图,已知线段及∠M,只用直尺和圆规,求作△ABC,使BC=a,∠B=∠M,∠C=2∠M(保留作图痕迹,不写作法) 如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.
如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.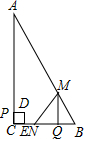 如图,在Rt△ABC中,AC=24cm,BC=12cm,动点P从点C出发,以1cm/s的速度沿CA方向向点A运动,同时点Q从点B出发,以1.5cm/s的速度沿BC方向向点C运动,当点Q到达终点时,点P也随之停止运动,过点Q作QM⊥BC,交AB于点M,以线段MQ为直角边在MQ的左侧作等腰直角△MQN,以线段CP为一边在△ABC内部作正方形PDEC,设运动时间为t(s),△MQN与正方形PDEC重叠部分的面积为S(cm2).
如图,在Rt△ABC中,AC=24cm,BC=12cm,动点P从点C出发,以1cm/s的速度沿CA方向向点A运动,同时点Q从点B出发,以1.5cm/s的速度沿BC方向向点C运动,当点Q到达终点时,点P也随之停止运动,过点Q作QM⊥BC,交AB于点M,以线段MQ为直角边在MQ的左侧作等腰直角△MQN,以线段CP为一边在△ABC内部作正方形PDEC,设运动时间为t(s),△MQN与正方形PDEC重叠部分的面积为S(cm2).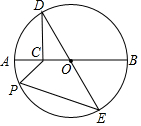 如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.
如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.