题目内容
7.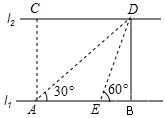 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.
分析 根据题意中的数据和锐角三角函数可以解答本题.
解答 解:由题意可得,
tan∠DAB=$\frac{DB}{AB}$,tan$∠DEB=\frac{DB}{BE}$,∠CAB=90°,∠DAB=30°,AE=60米,
∴$\frac{DB}{tan30°}-\frac{DB}{tan60°}$=60,
解得,DB=30$\sqrt{3}$米,
即河的宽度是30$\sqrt{3}$米.
点评 本题考查解直角三角形的应用,解答本题的关键是明确题意,利用锐角三角函数解答.

练习册系列答案
相关题目
12.判断下列几组数据中,可以作为直角三角形的三条边的是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
19.若a+b<0,$\frac{b}{a}$>0,则下列成立的是( )
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b<0 | D. | a<0,b>0 |
 如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.
如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.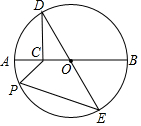 如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.
如图⊙O的半径为2,AB为直径.过AO的中点C作CD⊥AB交⊙O于点D,DE为⊙O的直径,点P为⊙O上动点,则2PC+PE的最小值是2$\sqrt{7}$.