题目内容
8.直角三角形两直角边分别为5cm和12cm,则其斜边的高为( )| A. | 6cm | B. | 8cm | C. | $\frac{80}{13}$cm | D. | $\frac{60}{13}$cm |
分析 根据勾股定理可求出斜边.然后由于同一三角形面积一定,可列方程直接解答.
解答 解:∵直角三角形的两条直角边分别为5cm,12cm,
∴斜边为:$\sqrt{{5}^{2}+1{2}^{2}}$=13cm,
设斜边上的高为hcm,则
$\frac{1}{2}$×5×12=$\frac{1}{2}$×13•h,
解得h=$\frac{60}{13}$.
故选:D.
点评 此题考查了勾股定理的运用即直角三角形的面积的求法,属中学阶段常见的题目,需同学们认真掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若a+b<0,$\frac{b}{a}$>0,则下列成立的是( )
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b<0 | D. | a<0,b>0 |
18.在实数0,(-$\sqrt{3}$)0,(-$\frac{2}{3}$)-2,|-2|中,最大的是( )
| A. | 0 | B. | (-$\sqrt{3}$)0 | C. | (-$\frac{2}{3}$)-2 | D. | |-2| |
 如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.
如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.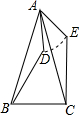 如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长.
如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长.