题目内容
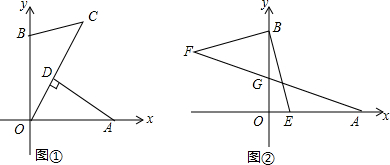
11.如图①,已知A(a,0),B(0,b),且a,b满足a2-8a+b2-8b=-32.(1)求A,B两点的坐标;
(2)若点C在第一象限内的一点,且∠OCB=45°,过A作AD⊥OC于D点,求证:AD=CD;
(3)如图②,若已知E(1,0),连接BE,过B作BF⊥BE且BF=BE,连接AF交y轴于G点,求G点的坐标.
分析 (1)由已知得(a-4)2+(b-4)2=0,根据非负数的性质即可解决问题.
(2)由O、A、C、B四点共圆得∠AOB+∠BCA=180°,得∠BCA=90°由此解决问题.
(3)先证明△BFM≌△EBO,求出BM、OM,再证明△FMG≌△AOG即可解决问题.
解答 (1)解:∵a2-8a+b2-8b=-32,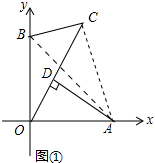
∴(a2-8a+16)+(b2-8b+16)=0,
∴(a-4)2+(b-4)2=0,
∵(a-4)2≥0,(b-4)2≥0,
∴a=b=4,
∴点A坐标为(4,0),点B坐标为(0,4).
(2)证明:∵点A坐标为(4,0),点B坐标为(0,4),
∴OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°,
∴∠BCO=∠BAO,
∴O、A、C、B四点共圆,
∴∠AOB+∠BCA=180°,
∵∠AOB=90°,
∴∠BCA=90°,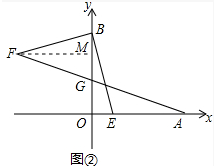
∴∠DCA=90°-∠BCA=45°,
∵AD⊥CD,
∴∠ADC=90°,∠DCA=∠DAC=45°,
∴DC=DA.
(3)解:作FM⊥OB于M,
∵∠FBM+∠OBE=90°,∠OBE+∠OEB=90°,
∴∠FBM=∠BEO,
在△FBM和△BEO中,
$\left\{\begin{array}{l}{∠FBM=∠BEO}\\{∠FMB=∠BOE=90°}\\{BF=BE}\end{array}\right.$,
∴△BFM≌△EBO,
∴FM=BO=AO,BM=OE=1,OM=3,
∵FM∥AO,
∴∠FMG=∠AOG,
在△FMG和△AOG中,
$\left\{\begin{array}{l}{∠FMG=∠AOG=90°}\\{∠FGM=∠AGO}\\{FM=AO}\end{array}\right.$,
∴△FMG≌△AOG,
∴MG=OG=$\frac{1}{2}$OM=$\frac{3}{2}$,
∴点M坐标(0,$\frac{3}{2}$).
点评 本题考查全等三角形的判定和性质、四点共圆、坐标与图形、非负数的性质等知识,第一个问题的关键是非负数性质的利用,第二个问题的关键是四点共圆,利用圆内接四边形的性质解决问题,第三个问题通过全等三角形解决问题,属于中考常考题型.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案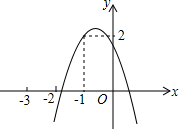 如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,-2<x1<-1,0<x2<1,下列结论:
如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;
②2a-b<0;
③b2+8a>4ac;
④b<-1.
其中正确的有 ( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲班 | 8 | 7 | 7 | 4 | 8 | 7 | 8 | 8 | 8 | 8 |
| 乙班 | 7 | 8 | 8 | 10 | 7 | 7 | 8 | 7 | 7 | 7 |
(2)采用怎样的方法,对参赛班级更为公平?若采用你提供的方法,甲、乙两班哪个班获胜?
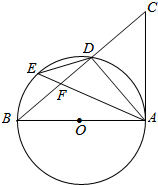 如图,AB是⊙O的直径,点D、E在⊙O上,连接AE、ED、DA,连接BD并延长至点C,使得∠DAC=∠AED.
如图,AB是⊙O的直径,点D、E在⊙O上,连接AE、ED、DA,连接BD并延长至点C,使得∠DAC=∠AED.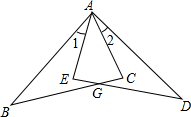 如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG.
如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG.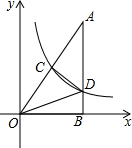 如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.
如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.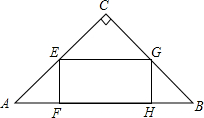 如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长. 如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.
如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.