题目内容
1. 如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.
如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.(1)求证:AE=BE;
(2)试求tan∠BAE的值.
分析 (1)先根据正方形和等边三角形的性质得出AD=DE,∠ADE=30°,求出∠DEA和∠CEB,由等腰三角形的性质求出∠DAE=75°,得出∠BAE=∠ABE,即可得出结论;
(2)延长AE交BC于M,作BN⊥AM于N,设BN=x,由三角形的外角性质得出∠BEN=30°,由含30°角的直角三角形的性质得出BE=2BN=2x,求出EN=$\sqrt{3}$x,得出AN,由三角函数的定义即可得出结果.
解答 (1)证明:∵四边形ABCD是正方形,△CDE是等边三角形,
∴AD=CD=BC,∠ADC=90°,DE=CD=CE,∠EDC=∠DEC=60°,
∴AD=DE=BC=CE,∠ADE=30°,
∴∠DAE=∠DEA,∠DEA=$\frac{1}{2}$(180°-30°)=75°,
∴∠DAE=75°,
∴∠BAE=90°-75°=15°,
同理:∠ABE=15°,
∴∠BAE=∠ABE,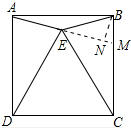 ∴AE=BE;
∴AE=BE;
(2)解:延长AE交BC于M,作BN⊥AM于N,如图所示:
设BN=x,
∵∠BEN=15°+15°=30°,
∴BE=2BN=2x,∴EN=$\sqrt{3}$x,
∴AN=(2+$\sqrt{3}$)x,
∴tan∠BAE=$\frac{BN}{AN}$=$\frac{x}{(2+\sqrt{3})x}$=2-$\sqrt{3}$.
点评 本题考查了正方形的性质、等边三角形的性质以及等腰三角形的性质;熟练掌握正方形和等边三角形的性质是解决问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
10. 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )| A. | 1 | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
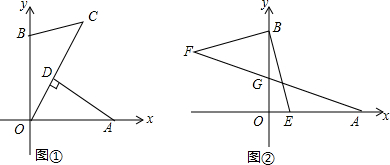
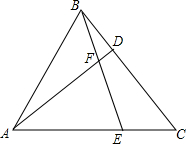 如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.
如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.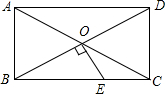 如图,?ABCD的对角线AC、BD交于点O,△AOB是等边三角形.
如图,?ABCD的对角线AC、BD交于点O,△AOB是等边三角形.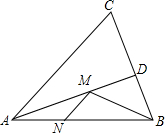 如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N是AD、AB上的动点,则BM+MN的最小值为3$\sqrt{3}$.
如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N是AD、AB上的动点,则BM+MN的最小值为3$\sqrt{3}$.