题目内容
6.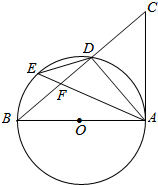 如图,AB是⊙O的直径,点D、E在⊙O上,连接AE、ED、DA,连接BD并延长至点C,使得∠DAC=∠AED.
如图,AB是⊙O的直径,点D、E在⊙O上,连接AE、ED、DA,连接BD并延长至点C,使得∠DAC=∠AED.(1)求证:AC是⊙O的切线;
(2)若点E是$\widehat{BD}$的中点,AE与BC交于点F,
①求证:CA=CF;
②当BD=5,CD=4时,DF=2.
分析 (1)欲证明AC是⊙O的切线,只需证得AB⊥AC即可;
(2)由圆周角、弧、弦间的关系即可推出CA=CF;
(3)通过相似三角形(△ADC∽△BAC)的对应边成比例求得AC=6.得出CA=CF=6,故DF=CA-CD=2.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠ABC+∠DAB=90°.
∵∠DAC=∠AED,∠AED=∠ABC,
∴∠DAC+∠DAB=90°,
∴AC是⊙O的切线.(3分)
(2)①证明:∵点E是$\widehat{BD}$的中点,
∴$\widehat{BE}$=$\widehat{DE}$,
∴∠BAE=∠DAE.
∵∠DAC+∠DAB=90°,∠ABC+∠DAB=90°,
∴∠DAC=∠ABC.
∵∠CFA=∠ABC+∠BAE,∠CAF=∠DAC+∠DAE,
∴∠CFA=∠CAF.
∴CA=CF.
②解:∵∠BAC=∠ADB=90°,
∴∠ACD=∠BCA,
∴△ADC∽△BAC.
∴$\frac{AC}{BC}$=$\frac{CD}{AC}$.即AC2=BC×CD=(5+4)×4=36.
解得AC=6.
∴CA=CF=6,
∴DF=CA-CD=2.
故答案为2.
点评 本题考查了切线的判定、相似三角形的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
16.下列多项式乘法中不能用平方差公式计算的是( )
| A. | (2x2y-1)(-2x2-1) | B. | (a3-b3)(b3-a3) | C. | (a+b)(a-b) | D. | (a2+b2)(b2-a2) |

 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上. 如图,在?ABCD中,AC是对角线,∠BAE=∠DAC,已知AB=7,AD=10,则CE=5.1.
如图,在?ABCD中,AC是对角线,∠BAE=∠DAC,已知AB=7,AD=10,则CE=5.1.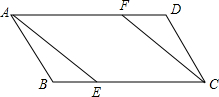 如图,在?ABCD中,已知点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.
如图,在?ABCD中,已知点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.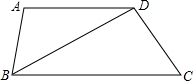 如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.
如图,在梯形ABCD中,AD∥BC,BD2=AD•BC,求证:△ADB∽△DBC.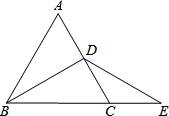 如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.