题目内容
1.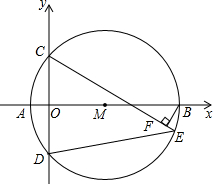 已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.
已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.(1)求m的值;
(2)求$\frac{CE-DE}{FE}$的值;
(3)若EF=$\frac{1}{2}$,求DE的值.
分析 (1)根据△>0可求出m的取值范围,然后运用根与系数的关系及条件就可求出m的值;
(2)连接EB并延长至点G,使得BG=DE,根据(1)中m的值,可求出OA、OB、AB、AM、CM,根据勾股定理可求出CO、CB,根据垂径定理可求出OD、CD,即可得到CD=CB,由此可证到△CDE≌△CBG,则有CE=CG,从而可证到△CEG是等边三角形,则有CE=EG,即可得到CE-DE=BE,只需求出FE与BE的数量关系即可;
(3)由条件可求出EF、BE,根据勾股定理可求出CF,从而可求出CE(即EG),即可求出BG(即DE),问题得以解决.
解答 解:(1)由题可得:
△=(2m-6)2-4×1×(m2-7)>0,①
x1+x2=-(2m-6),②
x1•x2=m2-7,③
x12+x22=10,④
解①得m<$\frac{8}{3}$.
由④得:x12+x22=(x1+x2)2-2x1•x2=(2m-6)2-2(m2-7)=10,
整理得m2-12m+20=0,
解得m1=2,m2=10.
∵m<$\frac{8}{3}$,
∴m=2;
(2)连接EB并延长至点G,使得BG=DE,如图所示.
当m=2时,原方程为x2-2x-3=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∴AB=4,OA=1,OB=3,
∴CM=AM=2,OM=1,
∴OC=$\sqrt{3}$,sin∠OMC=$\frac{\sqrt{3}}{2}$,
∴∠OMC=60°,
∴∠CMB=120°,
∴∠CEB=60°.
∵直径AB⊥CD,
∴OD=OC=$\sqrt{3}$,
∴CD=2$\sqrt{3}$.
在Rt△COB中,
BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{3+9}$=2$\sqrt{3}$,
∴CD=CB.
∵∠CDE+∠CBE=180°,∠CBG+∠CBE=180°,
∴∠CDE=∠CBG.
在△CDE和△CBG中,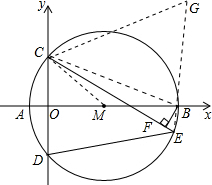
$\left\{\begin{array}{l}{CD=CB}\\{∠CDE=∠CBG}\\{DE=BG}\end{array}\right.$,
∴△CDE≌△CBG,
∴CE=CG.
∵∠CEG=60°,
∴△CEG是等边三角形,
∴CE=EG.
在Rt△BFE中,
cos∠FEB=$\frac{EF}{BE}$=$\frac{1}{2}$,
∴$\frac{CE-DE}{FE}$=$\frac{EG-BG}{FE}$=$\frac{BE}{FE}$=2;
(3)在Rt△CFB中,
∵BF=EF•tan60°=$\frac{1}{2}$×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,CB=2$\sqrt{3}$,
∴CF=$\sqrt{C{B}^{2}-B{F}^{2}}$=$\sqrt{12-\frac{3}{4}}$=$\frac{3\sqrt{5}}{2}$,
∴CE=$\frac{3\sqrt{5}}{2}$+$\frac{1}{2}$,
∴DE=BG=EG-BE=CE-BE=$\frac{3\sqrt{5}}{2}$+$\frac{1}{2}$-1=$\frac{3\sqrt{5}-1}{2}$.
点评 本题主要考查了根的判别式、根与系数的关系、等边三角形的判定与性质、圆内接四边形的对角互补、圆周角定理、三角函数、勾股定理等知识,构造三角形全等是解决第(2)小题的关键,需要注的意是运用根与系数的关系的前提是一元二次方程有根(即根的判别式非负).

| A. | 24x2y=3x•8xy | B. | m2-2m-3=m(m-2)-3 | C. | x2+2x+1=(x+1)2 | D. | (x+3)(x-3)=x2-9 |
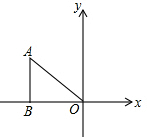 如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )
如图,Rt△ABO中,直角边BO落在x轴的负半轴上,点A的坐标是(-4,2),以O为位似中心,按比例尺1:2把△ABO缩小,则点A的对应点A′的坐标为( )| A. | (-1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,1)或(2,-1) |
 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.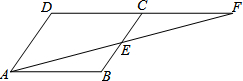 如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.
如图,?ABCD中,E是BC的中点,连结AE并延长交DC的延长线于F.试问:AB与CF相等吗?请说明理由.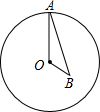 如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.
如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.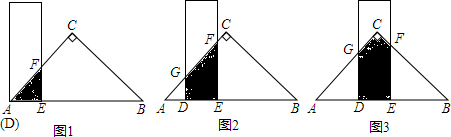
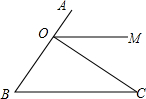 如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.
如图,已知∠B=50°,∠BOC=80°,OM平分∠AOC,求证:OM∥BC.