题目内容
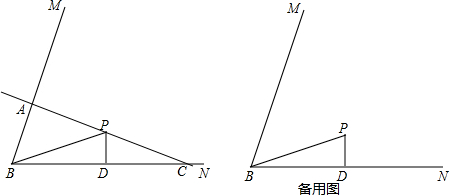
13.有一根直尺,短边的长为4cm,长边的长为10cm,还有一块锐角为45°的直角三角形纸板,它的斜边长16cm.如图1,将直尺的短边DE与直角三角形纸板的斜边AB重合,且点D与点A重合,将直尺沿AB方向平移,如图2,图3设平移的长度为x cm,且满足0≤x≤12,直尺与直角三角形纸板重合部分的面积(即图中阴影部分)为Scm2.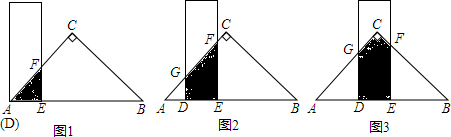
(1)当x=0时,S=8cm2;当x=4时,S=24cm2;当x=6时,S=28cm2.
(2)是否存在一个位置,使阴影部分的面积为26cm2?若存在,请求出此时x的值.
分析 (1)当x=0cm时,直尺和三角形纸板重叠部分的面积是两直角边都为4厘米的三角形面积;当x=4cm时,直尺和三角形纸板重叠部分的面积=两直角边都为8厘米的三角形面积-两直角边都为4厘米的三角形面积;当x=6cm时,直尺和三角形纸板重叠部分的面积=(两直角边都为8厘米的三角形面积-两直角边都为6厘米的三角形面积)×2,依此即可求解;
(2)根据阴影部分面积为26cm2,列出方程$\frac{1}{2}$(x+8)(8-x)+$\frac{1}{2}$(16-x-4+8)(4-8+x)=26,解方程即可求解.
解答 解:(1)当x=0cm时,S=4×4÷2=8cm2;
当x=4cm时,S=8×8÷2-4×4÷2=24cm2;
当x=6cm时,S=(8×8÷2-6×6÷2)×2=28cm2.
故答案为:8cm2;24cm2;28cm2.
(2)当S=26cm2时,x必然大于4,即$\frac{1}{2}$(x+8)(8-x)+$\frac{1}{2}$(16-x-4+8)(4-8+x)=26,
解得x1=6-$\sqrt{2}$,x2=6+$\sqrt{2}$.
故当x1=6-$\sqrt{2}$,x2=6+$\sqrt{2}$时,阴影部分面积为26cm2.
点评 本题考查了平移的性质,动点问题的函数图象,涉及的知识点有:直角三角形的面积,矩形的性质,梯形的面积,分类思想的应用,方程思想的应用,综合性较强,难度中等.

练习册系列答案
相关题目
5.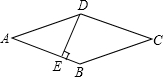 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.8 |
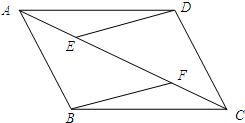 如图,在?ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,BF,求证:DE∥BF.
如图,在?ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,BF,求证:DE∥BF.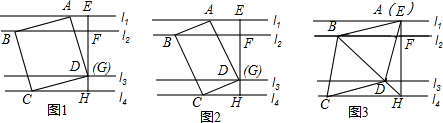
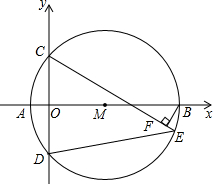 已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.
已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.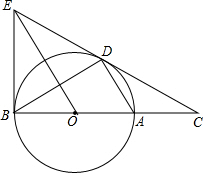 如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.