题目内容
5.阅读下面问题:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}-1$;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}-\sqrt{2}$;
$\frac{1}{\sqrt{5}+2}$=$\frac{1×(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\sqrt{5}$-2.
试求:(1)$\frac{1}{{\sqrt{7}+\sqrt{6}}}$=$\sqrt{7}$-$\sqrt{6}$;
(2)$\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$(n为正整数)=$\sqrt{n+1}$-$\sqrt{n}$.
(3)$\frac{1}{{1+\sqrt{2}}}+\frac{1}{{\sqrt{2}+\sqrt{3}}}+\frac{1}{{\sqrt{3}+\sqrt{4}}}+…+\frac{1}{{\sqrt{2014}+\sqrt{2015}}}+\frac{1}{{\sqrt{2015}+\sqrt{2016}}}$的值.
分析 (1)分子、分母都乘以$\sqrt{7}$-$\sqrt{6}$,分母有理化可得;
(2)分子、分母都乘以$\sqrt{n+1}$-$\sqrt{n}$,分母有理化可得;
(3)将原式按照以上规律拆开后两两抵消后即可得.
解答 解:(1)$\frac{1}{{\sqrt{7}+\sqrt{6}}}$=$\frac{1×(\sqrt{7}-\sqrt{6})}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}$-$\sqrt{6}$,
故答案为:$\sqrt{7}$-$\sqrt{6}$;
(2)$\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$=$\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$,
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(3)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2015}$-$\sqrt{2014}$+$\sqrt{2016}$-$\sqrt{2015}$
=$\sqrt{2016}$-1.
点评 本题主要考查二次根式的化简求值,熟练掌握二次根式中分母有理化及运用已知规律求值是解题的关键.

练习册系列答案
相关题目
13.已知菱形的周长为20,它的一条对角线长为6,则菱形的面积是( )
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
20.若a=9,b=16,则a,b的比例中项是( )
| A. | ±9 | B. | 12 | C. | -12 | D. | ±12 |
 如图,在Rt△ABC中,∠B=90°,AB<BC,分别以顶点A、C为圆心,以大于$\frac{1}{2}$AC长为半径作圆弧,两弧交于点MN,作直线MN,交边BC于点D,若BD=6,CD=10,则AB的长为8.
如图,在Rt△ABC中,∠B=90°,AB<BC,分别以顶点A、C为圆心,以大于$\frac{1}{2}$AC长为半径作圆弧,两弧交于点MN,作直线MN,交边BC于点D,若BD=6,CD=10,则AB的长为8.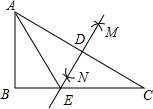 如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,过M,N两点作直线,与AC、BC分别交于点D、E.连接AE,则
如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,过M,N两点作直线,与AC、BC分别交于点D、E.连接AE,则 顶角为36°的等腰三角形称为“黄金三角形”,请你利用如图所示的黄金三角形求sin18°的值.
顶角为36°的等腰三角形称为“黄金三角形”,请你利用如图所示的黄金三角形求sin18°的值.