题目内容
2.已知一次函数y=-$\frac{1}{2}$x+3,求在这个函数的图象上且位于x轴上方的所有点的横坐标的取值范围.分析 先求出一次函数与x轴的交点坐标,然后根据一次函数的性质写出图象位于x轴上方的所有点的横坐标的取值范围.
解答 解:当y=0时,-$\frac{1}{2}$x+3=0,解得x=6,
因为当k=-$\frac{1}{2}$<0,y随x的增大而减小,
所以在这个函数的图象上且位于x轴上方的所有点的横坐标的取值范围为x<6.
点评 本题考查了一次函数函数的性质:对于y=kx+b,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小,当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.

练习册系列答案
相关题目
16.若x,y都是有理数,且|4-3x+y|与(3-4x-y)2互为相反数,则x,y的值分别为( )
| A. | x=-1,y=2 | B. | x=1,y=-1 | C. | x=0,y=-$\frac{3}{5}$ | D. | x=3,y=1 |
14.下列计算中,结果正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a6 | C. | (2a)(3a)=6a | D. | a6÷a2=a3 |
12.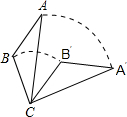 如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
 如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )
如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )| A. | $\frac{2}{3}$π | B. | $\frac{8}{3}$π | C. | 6π | D. | $\frac{10}{3}$π |
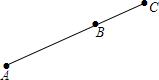 如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.
如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.