题目内容
1.某射手在相同条件下进行射击训练,结果如下表所示:| 射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
| 击中靶心次数m | 9 | 19 | 44 | 91 | 178 | 450 |
| 击中靶心频率$\frac{m}{n}$ |
(2)试根据该表,估计这名射手射击一次,击中靶心的概率约为多少?并说明理由.
分析 (1)根据表格中所给的样本容量和频数,求比值算出击中靶心的频率,填入表中.
(2)用频率来估计概率,频率一般都在0.90左右摆动,所以估计概率为0.90,这是概率与频率之间的关系,即用频率值来估计概率值.
解答 解:(1)填表如下:
| 射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
| 击中靶心次数m | 9 | 19 | 44 | 91 | 178 | 450 |
| 击中靶心频率$\frac{n}{m}$ | 0.90 | 0.95 | 0.88 | 0.91 | 0.89 | 0.90 |
点评 本题考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9.将抛物线y=3x2先向左平移1个单位,再向下平移4个单位,所得到的新抛物线是( )
| A. | y=3(x+1)2-4 | B. | y=3(x-1)2-4 | C. | y=3(x+1)2+4 | D. | y=3(x-1)2+4 |
16.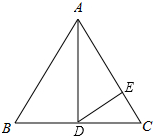 如图,在△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,DE⊥AC于点E,则tan∠CDE的值等于( )
如图,在△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,DE⊥AC于点E,则tan∠CDE的值等于( )
 如图,在△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,DE⊥AC于点E,则tan∠CDE的值等于( )
如图,在△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,DE⊥AC于点E,则tan∠CDE的值等于( )| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{5}{13}$ | D. | $\frac{10}{13}$ |
11.数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在数轴上画出一条长2015cm的线段AB,则AB盖住的整点个数是( )
| A. | 2015或2016 | B. | 2014或2015 | C. | 2016 | D. | 2015 |
 抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).
抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(3,0)两点,与y轴交于点C(0,-3).