题目内容
10.解方程(1)2x2+1=3x(配方法)
(2)x2-3$\sqrt{2}$x+3=0(公式法)
(3)解方程x2-|x|-2=0.
分析 (1)移项后把二次项系数化为1,然后进行配方,进而求出方程的根;
(2)首先找出方程a,b和c的值,求出△,代入求根公式即可;
(3)分x>0和x<0两种情况,利用因式分解法求出方程的根即可.
解答 解:(1)∵2x2+1=3x,
∴2x2-3x+1=0,
∴x2-$\frac{3}{2}$x+$\frac{1}{2}$=0,
∴x2-$\frac{3}{2}$x+$\frac{9}{16}$=$\frac{1}{16}$,
∴(x-$\frac{3}{4}$)2=$\frac{1}{16}$,
∴x-$\frac{3}{4}$=±$\frac{1}{4}$,
∴x1=1,x2=$\frac{1}{2}$;
(2)∵a=1,b=-3$\sqrt{2}$,c=3,
∴△=b2-4ac=18-12=6,
∴x=$\frac{3\sqrt{2}±\sqrt{6}}{2}$,
∴x1=$\frac{3\sqrt{2}+\sqrt{6}}{2}$,x2=$\frac{3\sqrt{2}-\sqrt{6}}{2}$;
(3)当x>0时,x2-x-2=0,
即(x-2)(x+1)=0,
解得x1=2,x2=-1(舍去),
当x<0时,x2+x-2=0,
即(x+2)(x-1)=0,
解得x3=-2,x4=1(舍去);
综上x=2或x=-2.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
1.某射手在相同条件下进行射击训练,结果如下表所示:
(1)计算并填写表中击中靶心的频率;
(2)试根据该表,估计这名射手射击一次,击中靶心的概率约为多少?并说明理由.
| 射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
| 击中靶心次数m | 9 | 19 | 44 | 91 | 178 | 450 |
| 击中靶心频率$\frac{m}{n}$ |
(2)试根据该表,估计这名射手射击一次,击中靶心的概率约为多少?并说明理由.
5.下列方程中,是关于x的一元二次方程的是( )
| A. | 2x2+2x=x(2x+2) | B. | 3x2+y=0 | C. | 5x2+$\frac{5}{x}$+3=0 | D. | (a2+2)x2-3x+2=0 |
15.计算a6(a2)3的结果等于( )
| A. | a11 | B. | a12 | C. | a14 | D. | a36 |
20.用配方法解方程x2+8x+9=0,变形后的结果正确的是( )
| A. | (x+4)2=-7 | B. | (x+4)2=-9 | C. | (x+4)2=7 | D. | (x+4)2=25 |
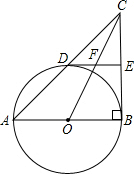 如图,Rt△ABC中,∠ABC=90°,以AB为直径作圆O交AC边于点D,E是边BC的中点,连结OC交DE于点F.
如图,Rt△ABC中,∠ABC=90°,以AB为直径作圆O交AC边于点D,E是边BC的中点,连结OC交DE于点F.