题目内容
16.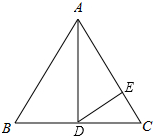 如图,在△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,DE⊥AC于点E,则tan∠CDE的值等于( )
如图,在△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,DE⊥AC于点E,则tan∠CDE的值等于( )| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{5}{13}$ | D. | $\frac{10}{13}$ |
分析 由△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,利用等腰三角形三线合一的性质,可证得AD⊥BC,再利用勾股定理,求得AD的长,那么在直角△ACD中根据三角函数的定义求出tan∠CAD,然后根据同角的余角相等得出∠CDE=∠CAD,于是tan∠CDE=tan∠CAD.
解答  解:∵△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,
解:∵△ABC中,AB=AC=13,AD为BC边上的中线,BC=10,
∴AD⊥BC,CD=$\frac{1}{2}$BC=5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=12,
∴tan∠CAD=$\frac{CD}{AD}$=$\frac{5}{12}$.
∵AD⊥BC,DE⊥AC,
∴∠CDE+∠ADE=90°,∠CAD+∠ADE=90°,
∴∠CDE=∠CAD,
∴tan∠CDE=tan∠CAD=$\frac{5}{12}$.
故选A.
点评 此题考查了解直角三角形、等腰三角形的性质、勾股定理、锐角三角函数的定义以及余角的性质.此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
相关题目
3.已知关于x,y的方程组$\left\{\begin{array}{l}{2x-ay=6}\\{4x+y=7}\end{array}\right.$有整数解,即x,y都是整数,a是正整数,求a的值.
1.某射手在相同条件下进行射击训练,结果如下表所示:
(1)计算并填写表中击中靶心的频率;
(2)试根据该表,估计这名射手射击一次,击中靶心的概率约为多少?并说明理由.
| 射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
| 击中靶心次数m | 9 | 19 | 44 | 91 | 178 | 450 |
| 击中靶心频率$\frac{m}{n}$ |
(2)试根据该表,估计这名射手射击一次,击中靶心的概率约为多少?并说明理由.
5.下列方程中,是关于x的一元二次方程的是( )
| A. | 2x2+2x=x(2x+2) | B. | 3x2+y=0 | C. | 5x2+$\frac{5}{x}$+3=0 | D. | (a2+2)x2-3x+2=0 |
6. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD等于( )
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD等于( )
 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD等于( )
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD等于( )| A. | 32° | B. | 64° | C. | 128° | D. | 148° |
 如图:
如图: