ÌâÄ¿ÄÚÈÝ
8£®¼ÆË㣺£¨1£©£¨x-y+$\frac{4xy}{x-y}$£©£¨x+y-$\frac{4xy}{x+y}$£©£»
£¨2£©£¨$\frac{x}{y}$-$\frac{y}{x}$£©¡Â£¨$\frac{x}{y}$+$\frac{y}{x}$-2£©¡Â£¨1+$\frac{y}{x}$£©£»
£¨3£©$\frac{2{x}^{2}-8{y}^{2}}{3y-2x}$¡Â$\frac{{x}^{2}-2xy}{4{x}^{2}-12xy+9{y}^{2}}$£®
·ÖÎö £¨1£©ÔʽÀ¨ºÅÖÐÁ½Ïîͨ·Ö²¢ÀûÓÃͬ·Öĸ·ÖʽµÄ¼Ó¼õ·¨Ôò¼ÆË㣬Լ·Ö¼´¿ÉµÃµ½½á¹û£»
£¨2£©ÔʽÀ¨ºÅÖÐÁ½Ïîͨ·Ö²¢ÀûÓÃͬ·Öĸ·ÖʽµÄ¼Ó¼õ·¨Ôò¼ÆË㣬ÀûÓóý·¨·¨Ôò±äÐΣ¬Ô¼·Ö¼´¿ÉµÃµ½½á¹û£»
£¨3£©ÔʽÀûÓóý·¨·¨Ôò±äÐΣ¬Ô¼·Ö¼´¿ÉµÃµ½½á¹û£®
½â´ð ½â£º£¨1£©Ôʽ=$\frac{£¨x-y£©^{2}+4xy}{x-y}$•$\frac{£¨x+y£©^{2}-4xy}{x+y}$=$\frac{£¨x+y£©^{2}£¨x-y£©^{2}}{£¨x+y£©£¨x-y£©}$=£¨x+y£©£¨x-y£©=x2-y2£»
£¨2£©Ôʽ=$\frac{{x}^{2}-{y}^{2}}{xy}$¡Â$\frac{{x}^{2}+{y}^{2}-2xy}{xy}$¡Â$\frac{x+y}{x}$=$\frac{£¨x+y£©£¨x-y£©}{xy}$•$\frac{xy}{£¨x-y£©^{2}}$•$\frac{x}{x+y}$=$\frac{x}{x-y}$£»
£¨3£©Ôʽ=$\frac{2£¨x+2y£©£¨x-2y£©}{-£¨2x-3y£©}$•$\frac{£¨2x-3y£©^{2}}{x£¨x-2y£©}$=-$\frac{2£¨x+2y£©£¨2x-3y£©}{x}$£®
µãÆÀ ´ËÌ⿼²éÁË·ÖʽµÄ»ìºÏÔËË㣬ÊìÁ·ÕÆÎÕÔËËã·¨ÔòÊǽⱾÌâµÄ¹Ø¼ü£®

Á·Ï°²áϵÁдð°¸
 ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸
ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸ СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸
СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸
Ïà¹ØÌâÄ¿
1£®Ä³ÉäÊÖÔÚÏàͬÌõ¼þϽøÐÐÉä»÷ѵÁ·£¬½á¹ûÈçϱíËùʾ£º
£¨1£©¼ÆËã²¢Ìîд±íÖл÷ÖаÐÐĵÄƵÂÊ£»
£¨2£©ÊÔ¸ù¾Ý¸Ã±í£¬¹À¼ÆÕâÃûÉäÊÖÉä»÷Ò»´Î£¬»÷ÖаÐÐĵĸÅÂÊԼΪ¶àÉÙ£¿²¢ËµÃ÷ÀíÓÉ£®
| Éä»÷´ÎÊýn | 10 | 20 | 50 | 100 | 200 | 500 |
| »÷ÖаÐÐÄ´ÎÊým | 9 | 19 | 44 | 91 | 178 | 450 |
| »÷ÖаÐÐÄƵÂÊ$\frac{m}{n}$ |
£¨2£©ÊÔ¸ù¾Ý¸Ã±í£¬¹À¼ÆÕâÃûÉäÊÖÉä»÷Ò»´Î£¬»÷ÖаÐÐĵĸÅÂÊԼΪ¶àÉÙ£¿²¢ËµÃ÷ÀíÓÉ£®
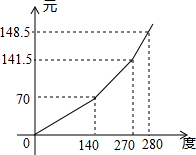 Î人ÊÐ2012Äê4Ô¾ÓÃñÓõç×¼±¸ÊµÐн×Ìݵç¼Û£¬µÚÒ»µµÎª140¡ãÒÔÄÚ¼Û¸ñ²»±ä£¬µÚ¶þµµÎª140¡ã-270¡ã¼Û¸ñ΢µ÷£¬µÚÈýµµ³¬¹ý270¡ãÒÔÉϼ۸ñÔÙ¼ÓÒ»µã£¬Ã¿¸öÔµĵç·Ñy£¨Ôª£©ÓëÓõçÁ¿x£¨¶È£©µÄº¯Êý¹ØϵÈçͼËùʾ£¬Èôij¾ÓÃñ9Ô·ÝÓõç300¶È£¬µç·Ñµ÷Õûºó½«¶àÖ§³ö12.5Ôª£®
Î人ÊÐ2012Äê4Ô¾ÓÃñÓõç×¼±¸ÊµÐн×Ìݵç¼Û£¬µÚÒ»µµÎª140¡ãÒÔÄÚ¼Û¸ñ²»±ä£¬µÚ¶þµµÎª140¡ã-270¡ã¼Û¸ñ΢µ÷£¬µÚÈýµµ³¬¹ý270¡ãÒÔÉϼ۸ñÔÙ¼ÓÒ»µã£¬Ã¿¸öÔµĵç·Ñy£¨Ôª£©ÓëÓõçÁ¿x£¨¶È£©µÄº¯Êý¹ØϵÈçͼËùʾ£¬Èôij¾ÓÃñ9Ô·ÝÓõç300¶È£¬µç·Ñµ÷Õûºó½«¶àÖ§³ö12.5Ôª£®