题目内容
8．
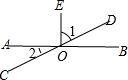如图，直线AB和CD相交于O点，∠EOB=90°，则图中∠1与∠2的关系是（ ）| A． | ∠1与∠2互补 | B． | ∠1与∠2互余 | C． | ∠1与∠2相等 | D． | ∠1=2∠2 |
分析 根据对顶角相等得出∠DOB=∠2，再利用互余得出关系．
解答 解：因为∠DOB=∠2，
∠1+∠DOB=90°，
所以∠1与∠2的关系是互余，
故选B．
点评 此题考查对顶角问题，关键是根据对顶角的两边互为反向延长线且相等．
练习册系列答案
相关题目
19．
如图，一次函数y=-kx+n（k≠0）与x轴、y轴分别交于A、B两点，与反比例函数y=$\frac{k}{x}$（k≠0）交于C、D两点，且C、D两点分别是线段AB的三等分点，若S△AOB=$\frac{9}{4}$，则n=（ ）
如图，一次函数y=-kx+n（k≠0）与x轴、y轴分别交于A、B两点，与反比例函数y=$\frac{k}{x}$（k≠0）交于C、D两点，且C、D两点分别是线段AB的三等分点，若S△AOB=$\frac{9}{4}$，则n=（ ）| A． | -$\sqrt{2}$ | B． | -$\frac{3}{2}\sqrt{2}$ | C． | -2$\sqrt{2}$ | D． | -$\frac{5}{2}\sqrt{2}$ |
如图所示，有以下三个条件：①AC=AB，②AB∥CD，③∠1=∠2，从这三个条件中任选两个作为假设，另一个作为结论，则组成真命题的个数为（ ）
如图，直线l1、l2、…l6是一组等距离的平行线，过直线l1上的点A作两条射线，分别与直线l3，l6相交于点B、E、C、F．若BC=2，则EF的长是（ ）
18．二次函数y=ax2+bx+c（a，b，c是常数，且a≠0）中的x与y的部分对应值如下表所示，则下列结论中，正确的个数有（ ）
（1）a＜0；
（2）当x＜0时，y＜3；
（3）当x＞1时，y的值随x值的增大而减小；
（4）方程ax2+bx+c=5有两个不相等的实数根．
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
（2）当x＜0时，y＜3；
（3）当x＞1时，y的值随x值的增大而减小；
（4）方程ax2+bx+c=5有两个不相等的实数根．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |