题目内容
12.已知矩形ABCD中,AB=3cm,AD=4cm,点E、F分别在边AD、BC上,连接B、E,D、F.分别把Rt△BAE和Rt△DCF沿 BE,DF折叠成如图所示位置.(1)若得到四边形 BFDE是菱形,求AE的长.
(2)若折叠后点A′和点C′恰好落在对角线BD上,求AE的长.

分析 (1)由矩形的性质得出∠A=90°,设AE=xcm,则ED=(4-x)cm,由菱形的性质得出EB=ED=4-x,由勾股定理得出方程,解方程即可;
(2)由勾股定理求出BD,由折叠的性质得出A′E=AE,∠EA′B=∠A=90°,A′B=AB=3cm,求出A′D,设AE=A′E=x,则ED=(4-x)cm,在Rt△EA′D中,由勾股定理得出方程,解方程即可.
解答 解:(1)∵四边形ABCD是矩形,
∴∠A=90°,
设AE=xcm,则ED=(4-x)cm,
∵四边形EBFD是菱形,
∴EB=ED=4-x,
由勾股定理得:AB2+AE2=BE2,
即32+x2=(4-x)2,
解得:x=$\frac{7}{8}$,
∴AE=$\frac{7}{8}$cm;
(2)根据勾股定理得:BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=5cm,
由折叠的性质得:A′E=AE,∠EA′B=∠A=90°,A′B=AB=3cm,
∴∠EA′D=90°,A′D=5-3=2(cm),
设AE=A′E=x,则ED=(4-x)cm,
在Rt△EA′D中,A′E2+A′D2=ED2,
即x2+22=(4-x)2,
解得:x=$\frac{3}{2}$,
∴AE=$\frac{3}{2}$cm.
点评 本题考查了翻折变换的性质、矩形的性质、勾股定理、菱形的性质;熟练掌握翻折变换和矩形、菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
2.已知甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷)
经计算,甲乙的平均数均为10,试根据这组数据估计乙种水稻品种的产量较稳定.
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| 乙 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
3. 如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若BC长6cm,则CC1的长为( )
如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若BC长6cm,则CC1的长为( )
 如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若BC长6cm,则CC1的长为( )
如图,△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的,若BC长6cm,则CC1的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
7.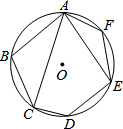 如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
 如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )
如图,在⊙O的内接六边形ABCDEF中,∠CAE=80°,则∠B+∠F的度数为( )| A. | 220° | B. | 240° | C. | 260° | D. | 280° |
17.若ab<0,$\frac{n}{m}$<0,则一次函数y=$\frac{a}{b}$x+mn一定不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,一只小鸟自由自在的在空中飞翔,然后随意落在如图所示的图形表示的空地上(每个方格除颜色外完全相同),则落在图中阴影部分的概率是$\frac{5}{16}$.
如图,一只小鸟自由自在的在空中飞翔,然后随意落在如图所示的图形表示的空地上(每个方格除颜色外完全相同),则落在图中阴影部分的概率是$\frac{5}{16}$.