题目内容
20.因式分解:(1)m2(a-b)+n2(b-a);
(2)x4-8x2+16.
分析 (1)原式变形后,提取公因式,再利用平方差公式分解即可;
(2)原式利用完全平方公式及平方差公式分解即可.
解答 解:(1)m2(a-b)+n2(b-a)
=m2(a-b)-n2(a-b)
=(a-b)(m2-n2)
=(a-b)(m+n)(m-n);
(2)x4-8x2+16
=(x2-4)2
=(x+2)2(x-2)2.
点评 此题考查了提公式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
15.下列各式中,正确的是( )
| A. | m5•m5=2m10 | B. | m4•m4=m8 | C. | m3•m3=m9 | D. | m6+m6=2m12 |
5.利用配方法将x2-2x+3=0化为a(x-h)2+k=0 (a≠0)的形式为 ( )
| A. | (x-1)2-2=0 | B. | (x-1)2+2=0 | C. | (x+1)2+2=0 | D. | (x+1)2-2=0 |
10.一组数据x1,x2,x3,…,xn的平均数是a,方差是b,那么数据2x1,2x2,2x3…2xn的平均数和方差分别是( )
| A. | 2a和2b | B. | 2a和4b | C. | 4a和2b | D. | 4a和4b |
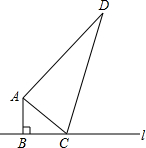 如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?
如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形? 如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长和∠ACB的度数.
如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长和∠ACB的度数.
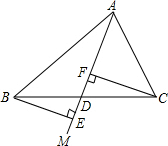 如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).
如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).