题目内容
1.化简:|a-b|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=0(其中a>0,b<0)分析 利用a,b的符号得出a-b的符号,进而利用绝对值和二次根式的性质化简求出即可.
解答 解:∵a>0,b<0,
∴a-b>0,
∴|a-b|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=a-b-a+b=0.
故答案为:0.
点评 此题主要考查了二次根式的性质与化简,正确得出a-b的符号是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列四个命题中,真命题是( )
| A. | 若一个角的两边分别平行于另一个角的两边,则这两个角相等 | |
| B. | 如果两个角的和是180°,那么这两个角是邻补角 | |
| C. | 在同一平面内,平行于同一条直线的两条直线互相平行 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线互相垂直 |
10.一组数据x1,x2,x3,…,xn的平均数是a,方差是b,那么数据2x1,2x2,2x3…2xn的平均数和方差分别是( )
| A. | 2a和2b | B. | 2a和4b | C. | 4a和2b | D. | 4a和4b |
 如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长和∠ACB的度数.
如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长和∠ACB的度数.
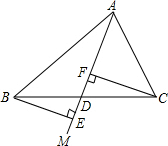 如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).
如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).