题目内容
4. 如图,一只小鸟自由自在的在空中飞翔,然后随意落在如图所示的图形表示的空地上(每个方格除颜色外完全相同),则落在图中阴影部分的概率是$\frac{5}{16}$.
如图,一只小鸟自由自在的在空中飞翔,然后随意落在如图所示的图形表示的空地上(每个方格除颜色外完全相同),则落在图中阴影部分的概率是$\frac{5}{16}$.
分析 根据几何概率的求法:小鸟落在阴影部分的概率就是阴影区域的面积与总面积的比值.
解答 解:设每个小正方形的边长为1,
由图可知:阴影部分面积为:$\frac{1}{2}$×2×2+$\frac{1}{2}$×1×2+$\frac{1}{2}$×1×4=5
所以图中阴影部分占5个小正方形,其面积占总面积的$\frac{5}{16}$,
所以其概率为$\frac{5}{16}$.
故答案为:$\frac{5}{16}$.
点评 本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
15.下列各式中,正确的是( )
| A. | m5•m5=2m10 | B. | m4•m4=m8 | C. | m3•m3=m9 | D. | m6+m6=2m12 |
16.下列四个命题中,真命题是( )
| A. | 若一个角的两边分别平行于另一个角的两边,则这两个角相等 | |
| B. | 如果两个角的和是180°,那么这两个角是邻补角 | |
| C. | 在同一平面内,平行于同一条直线的两条直线互相平行 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线互相垂直 |

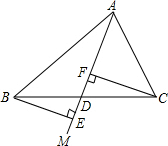 如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).
如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).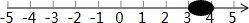 把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.
把无理数$\sqrt{17}$,$\sqrt{11}$,$\sqrt{5}$,$-\sqrt{3}$表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是$\sqrt{11}$.