题目内容
2.已知甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷)| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| 乙 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
分析 根据方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]分别求出两种水稻的产量的方差,再进行比较即可.
解答 解:甲种水稻产量的方差是:$\frac{1}{5}$[(9.4-10)2+(10.3-10)2+(10.8-10)2+(9.7-10)2+(9.8-10)2]=0.244.
乙种水稻产量的方差是:$\frac{1}{5}$[(9.8-10)2+(9.9-10)2+(10.1-10)2+(10-10)2+(10.2-10)2]=0.02,
∴0.02<0.244,
∴产量比较稳定的水稻品种是乙.
故答案为:乙.
点评 此题考查了方差,用到的知识点是方差和平均数的计算公式,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
17.下列说法中正确的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 同位角相等 | |
| C. | 垂直于同一条直线的两条直线互相平行 | |
| D. | 对顶角相等 |
7.某公司招聘人才,对应聘者分别进行阅读能力、专业知识、表达能力三项测试,并将三项测试得分按3:5:2的比例确定每人的最终成绩,现欲从甲乙两选手中录取一人,已知两人的各项测试得分如下表(单位:分)
①请通过相关的计算说明谁将被录用?
②请对落选者今后的应聘提些合理的建议.
| 阅读 | 专业 | 表达 | |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
②请对落选者今后的应聘提些合理的建议.
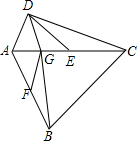 如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,
如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,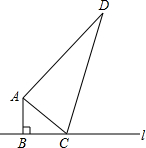 如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?
如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形? 如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长和∠ACB的度数.
如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9,求AB的长和∠ACB的度数.