题目内容
8.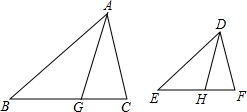 已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
分析 先根据三组对应边的比相等的两个三角形相似可判断△ABG∽△DEH,则∠B=∠E,∠BAG=∠EDH,再利用角平分线定义得到∠BAG=$\frac{1}{2}$∠BAC,∠EDH=$\frac{1}{2}$∠EDF,所以∠BAC=∠EDF,然后根据有两组角对应相等的两个三角形相似可得△DEF∽△ABC.
解答 证明:∵$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,
∴△ABG∽△DEH,
∴∠B=∠E,∠BAG=∠EDH,
而AG、DH分别是△ABC和△DEF的角平分线,
∴∠BAG=$\frac{1}{2}$∠BAC,∠EDH=$\frac{1}{2}$∠EDF,
∴∠BAC=∠EDF,
而∠B=∠C,
∴△DEF∽△ABC.
点评 本题考了相似三角形的判定:三组对应边的比相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
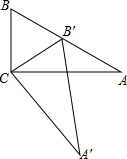 如图,在△ABC中,∠ACB=90°,∠B=60°,以C为旋转中心,旋转一定角度后成△A′B′C,此时B′落在斜边AB上,试确定∠ACA′,∠BB′C的度数.
如图,在△ABC中,∠ACB=90°,∠B=60°,以C为旋转中心,旋转一定角度后成△A′B′C,此时B′落在斜边AB上,试确定∠ACA′,∠BB′C的度数.
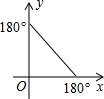
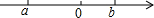 已知a,b两数在数轴上的位置如图所示,化简|a+b|+|a|-|a-b|.
已知a,b两数在数轴上的位置如图所示,化简|a+b|+|a|-|a-b|.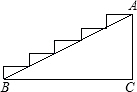 如图:在一个高6米,长10米的楼梯表面铺地毯,则该地毯的长度至少是14米.
如图:在一个高6米,长10米的楼梯表面铺地毯,则该地毯的长度至少是14米. 如图,在△ABC中,AB=2,BC=3,∠B=60°,将△ABC绕点A按顺时针方向旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CE的长为$\sqrt{7}$.
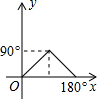
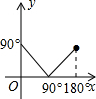
如图,在△ABC中,AB=2,BC=3,∠B=60°,将△ABC绕点A按顺时针方向旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CE的长为$\sqrt{7}$.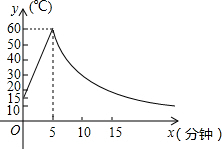 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.