题目内容
16.已知关于x的方程x2-(m2+3)x+$\frac{1}{2}$(m2+2)=0(1)证明:无论m是任何实数,方程总有两个正根;
(2)设x1,x2为方程的两根,且满足x${\;}_{1}^{2}$+x${\;}_{2}^{2}$-x1x2=$\frac{17}{2}$,求m值.
分析 (1)设方程的两个实数根为x1、x2,根据△≥0恒成立,x1•x2>0.x1+x2>0恒成立,即可证明.
(2)由方程的两个实数根为x1、x2,根据根与系数的关系即可解答
解答 解:(1)设方程的两个实数根为x1、x2,
△=(m2+3)2-4×$\frac{1}{2}$(m2+2)=m4+4m2+5=(m2+2)2+1≥0恒成立,
x1•x2=$\frac{1}{2}$(m2+2)>0恒成立,
x1+x2=m2+3>0恒成立,
∴无论m是任何实数,方程总有两个正根;
(2)∵x${\;}_{1}^{2}$+x${\;}_{2}^{2}$-x1x2=$\frac{17}{2}$,
∴(x1+x2)2-3x1x2=$\frac{17}{2}$,
∴(m2+3)2-3×$\frac{1}{2}$(m2+2)=$\frac{17}{2}$,
整理得:(2m2-1)(m2+5)=0
解得:m=±$\frac{\sqrt{2}}{2}$.
点评 本题考查了根与系数的关系及根的判别式,关键掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
6.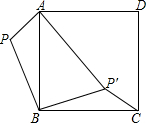 如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
 如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )
如图,已知P为正方形ABCD外的一点,PA=1,PB=2,将△ABP绕点B顺时针旋转90°,使点P旋转至点P′,且AP′=3,则∠BP′C的度数为 ( )| A. | 105° | B. | 112.5° | C. | 120° | D. | 135° |
1.用m个正方形和n个正八边形铺设地面,则m、n满足的条件是( )
| A. | 2m+3n=8 | B. | 3m+2n=8 | C. | m+n=4 | D. | m+2n=6 |
18.为了应对期末考试,老师布置了15道选择题作业,批阅后得到如下统计表,根据表中数据可知,由45名学生答对题数组成的样本的中位数是14.
| 答对题数(道) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 18 | 16 | 7 |
 如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.
如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.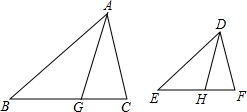 已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.