题目内容
10.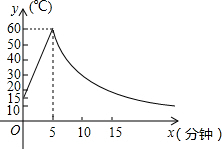 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
(3)该种材料温度维持在40℃以上(包括40℃)的时间有多长?
分析 (1)分成0≤x≤5和x>5两种情况,利用待定系数法即可求解;
(2)在当x>5时的函数解析式中,求得y=15时对应的自变量x的取值即可;
(3)在两个函数解析式中求得y=40时对应的自变量的值,求差即可.
解答 解:(1)当0≤x≤5时,
设函数的解析式是y=kx+b,则$\left\{\begin{array}{l}{b=15}\\{5k+b=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=15}\\{k=9}\end{array}\right.$
则函数的解析式是:y=9x+15;
$当x>5时,y=\frac{300}{x}$;
(2)把y=15代入$y=\frac{300}{x}$,得$15=\frac{300}{x}$,x=20;
经检验:x=20是原方程的解.
则当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了20分钟;
(3)把y=40代入y=9x+15得x=$\frac{25}{9}$;把y=40代入$y=\frac{300}{x}$得x=7.5,
所以材料温度维持在40℃以上(包括40℃)的时间为7.5-$\frac{25}{9}$=$\frac{85}{18}$分钟.
点评 本题考查了二次函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
相关题目
1.菱形的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
18.为了应对期末考试,老师布置了15道选择题作业,批阅后得到如下统计表,根据表中数据可知,由45名学生答对题数组成的样本的中位数是14.
| 答对题数(道) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 18 | 16 | 7 |
5.如果代数式$\frac{x-3}{\sqrt{x-2}}$有意义,那么x的取值范围是( )
| A. | x≥2 | B. | x>2且x≠3 | C. | x>2 | D. | x≥2且x≠3 |
2.点P(-1,3)向上平移1个单位长度后,再向左平移2个单位长度得到对应点Q,则Q点坐标是( )
| A. | (0,1) | B. | (-3,4) | C. | (2,1) | D. | (1,2) |
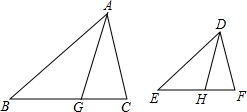 已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.