题目内容
12.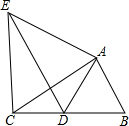 如图,在△ABC中,AB=2,BC=3,∠B=60°,将△ABC绕点A按顺时针方向旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CE的长为$\sqrt{7}$.
如图,在△ABC中,AB=2,BC=3,∠B=60°,将△ABC绕点A按顺时针方向旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CE的长为$\sqrt{7}$.
分析 根据旋转的性质得AD=AB,由∠B=60°,于是可判断△ADB为等边三角形,根据等边三角形的性质得BD=AB=3,然后利用CD=BC-BD进行计算可求出CD的长,过E作BC的垂线,交BC的延长线于点F,利用勾股定理即可求出CE的长.
解答 解:
过E作BC的垂线,交BC的延长线于点F,
∵△ABC绕点A按顺时针旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上,
∴AD=AB,
∵∠B=60°,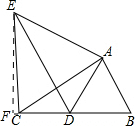
∴△ADB为等边三角形,
∴BD=AB=2,
∴CD=BC-BD=3-2=1.
∵∠B=∠ADE=60°,
∴∠EDF=60°,
∴∠DEF=30°,
∵DE=BC=3,
∴DF=1.5,EF=$\frac{3\sqrt{3}}{2}$,
∴CF=0.5,
∴CE=$\sqrt{E{F}^{2}+C{F}^{2}}$=$\sqrt{7}$,
故答案为$\sqrt{7}$.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.菱形的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
2.点P(-1,3)向上平移1个单位长度后,再向左平移2个单位长度得到对应点Q,则Q点坐标是( )
| A. | (0,1) | B. | (-3,4) | C. | (2,1) | D. | (1,2) |
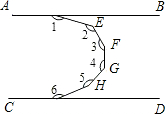 如图,两直线AB,CD平行,求∠1+∠2+∠3+∠4+∠5+∠6的值.
如图,两直线AB,CD平行,求∠1+∠2+∠3+∠4+∠5+∠6的值. 如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.
如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.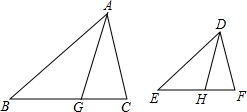 已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.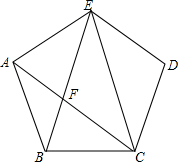 如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$.
如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$.