题目内容
9.先化简,再求值:$(1-\frac{1}{a})÷\frac{{{a^2}-1}}{a}-\frac{2a+2}{{{a^2}+2a+1}}$,a取-1、0、1、2中的一个数.分析 先化简,确定a的值,再代入求解即可.
解答 解::$(1-\frac{1}{a})÷\frac{{{a^2}-1}}{a}-\frac{2a+2}{{{a^2}+2a+1}}$
=$\frac{a-1}{a}$×$\frac{a}{(a+1)(a-1)}$-$\frac{2(a+1)}{(a+1)^{2}}$,
=$\frac{1}{a+1}$-$\frac{2}{a+1}$,
=-$\frac{1}{a+1}$,
∵由分式有意义的条件可得a≠-1、0、1,
∴a=2时,原式=-$\frac{1}{2+1}$=-$\frac{1}{3}$.
点评 本题主要考查了分式的化简求值,解题的关键是正确的化简.

练习册系列答案
相关题目
1.菱形的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
18.为了应对期末考试,老师布置了15道选择题作业,批阅后得到如下统计表,根据表中数据可知,由45名学生答对题数组成的样本的中位数是14.
| 答对题数(道) | 12 | 13 | 14 | 15 |
| 人数 | 4 | 18 | 16 | 7 |
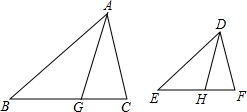 已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.