题目内容
19.△ABC内接于⊙O,记∠A=x,∠OBC=y,则y关于x的函数图象大致是( )| A. | 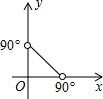 | B. | 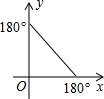 | C. | 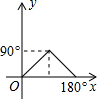 | D. | 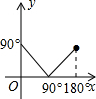 |
分析 分类讨论:当x≤90°时,根据圆周角定理得∠BOC=2x,然后利用等腰三角形的性质和三角形内角和得∠OBC=90°-x;当90°<x<180°时,根据圆内接四边形的性质得∠BOC=2(180°-x),再利用等腰三角形的性质和三角形内角和得∠OBC=$\frac{1}{2}$[180°-2(180°-x)]=x-90°,最后根据y与x的关系式对各选项进行判断.
解答 解:如图, 当x≤90°时,∠BOC=2x,则∠OBC=$\frac{1}{2}$(180°-2x)=90°-x;
当x≤90°时,∠BOC=2x,则∠OBC=$\frac{1}{2}$(180°-2x)=90°-x;
当90°<x<180°时,∠BOC=2(180°-x),则∠OBC=$\frac{1}{2}$[180°-2(180°-x)]=x-90°.
故选D.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了函数图象.

练习册系列答案
相关题目
1.菱形的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
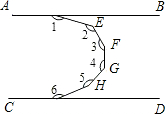 如图,两直线AB,CD平行,求∠1+∠2+∠3+∠4+∠5+∠6的值.
如图,两直线AB,CD平行,求∠1+∠2+∠3+∠4+∠5+∠6的值. 如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.
如图,DE是△ABC的AB、AC两边中点的连线,M是DE的中点,CM的延长线交AB于点N,则S△DMN:S四边形ANME=1:5.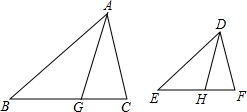 已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.
已知,如图,AG、DH分别是△ABC和△DEF的角平分线,且$\frac{AB}{DE}$=$\frac{BG}{EH}$=$\frac{AG}{DH}$,求证:△DEF∽△ABC.